Equation et complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 18:53
par Silver53 » 13 Oct 2006, 18:53
Bonjour!
le professeur nous a dit que l'équation suivante était longue à résoudre. Je voudrait que vous me donniez des pistes.
[(z²+1)/(z²-1)]^8 = 1
merci
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 13 Oct 2006, 19:22
par Quidam » 13 Oct 2006, 19:22
Silver53 a écrit:Bonjour!
le professeur nous a dit que l'équation suivante était longue à résoudre. Je voudrait que vous me donniez des pistes.
[(z²+1)/(z²-1)]^8 = 1
merci
Pose
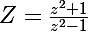
et résouds d'abord l'équation en Z !
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 20:11
par Silver53 » 13 Oct 2006, 20:11
Si je pose

alors l'équation
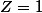
admet 8 solutions qui sont les 8 racines huitième de 1 c'est bien ça? Si oui que dois-je ensuite faire?
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 13 Oct 2006, 20:35
par Imod » 13 Oct 2006, 20:35
Pour chacune des huit solutions que tu as trouvé , tu dois trouver les deux solutions de l'équation du 2ème degré que tu obtiens , un travail de titan :mur:
Imod
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 21:07
par Silver53 » 13 Oct 2006, 21:07
Ok donc si j'ai bien compris il y a au maximum 16 solutions, et ce n'est pas très compliqué, c'est surtout long à faire! Je vais commencer ce soir alors :mur:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Oct 2006, 21:14
par abcd22 » 13 Oct 2006, 21:14
Bonsoir,
Comme toutes les solutions que tu trouves pour Z sont de la forme
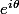
, tu peux commencer à résoudre
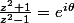
et ne remplacer

par des valeurs que quand c'est nécessaire.
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 21:31
par Silver53 » 13 Oct 2006, 21:31
je ne comprend pas très bien ta méthode abcd22
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Oct 2006, 21:50
par abcd22 » 13 Oct 2006, 21:50
On commence par écrire z² = quelque chose qui dépend de

si
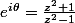
, et on remplace

par les 8 valeurs possibles (telles que
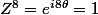
) pour calculer les racines, ça évite de faire 8 fois le même calcul.
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 21:51
par Silver53 » 13 Oct 2006, 21:51
Si je pose
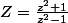
, pour trouver le module de

dois-je remplacer

par
)
? puis ensuite simplifier

, et trouver son argument?
abcd22 merci mais je ne comprends pas trop ta méthode et je suis censé le résoudre avec des notions déjà vues en cours ou en TD. Cela ne me dérange pas de faire 8 calculs, ce que je veux, c'est savoir faire cet exo et comprendre afin de pouvoir le refaire. Donc si tu pouvais m'aider avec la méthode de Imod ça serait :++:
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Oct 2006, 21:58
par abcd22 » 13 Oct 2006, 21:58
Tu as dit plus haut que les solutions pour Z étaient les 8 racines de 1, qui sont de la forme

, maintenant qu'on a Z c'est z qu'on cherche (pour chaque valeur possible de Z), ce n'est pas très dur de trouver z² en fonction de Z, ensuite il faut calculer les racines carrées.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Oct 2006, 21:59
par abcd22 » 13 Oct 2006, 21:59
Je ne te propose pas une méthode différente de celle de lmod mais juste de « factoriser » des calculs pour éviter de les écrire 8 fois.
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 22:13
par Silver53 » 13 Oct 2006, 22:13
Je sais seulement que les 8 solutions sont de la forme
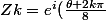)
avec
})
(edit: j'avais fais une erreur)
ensuite pour

par exemple,
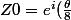)
j'en déduis que

?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Oct 2006, 22:15
par abcd22 » 13 Oct 2006, 22:15
Pourquoi tu mets un theta dans tes racines de l'unité ?
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 22:21
par Silver53 » 13 Oct 2006, 22:21
Oula effectivement j'enchaine les erreurs. Je reprends, les 8 racines huitième de 1 sont de la forme :
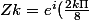)
donc par exemple pour k=0 on a
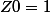
. Dois-je en déduire que les deux premières solutions de l'équation de départ vérifient

=1 ???
car si oui j'en déduis que
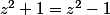
:hum:
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 13 Oct 2006, 23:12
par Silver53 » 13 Oct 2006, 23:12
Quand je le fais pour Z0, je ne trouve aucune solution. Quand je le fais pour Z1, je trouve
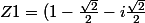z^2 + (1+\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2})=0)
et j'en déduis des valeurs invraissemblables du genre
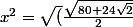)
quand je cherche les deux racines du trinome.
SVP aidez moi
merci
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 14 Oct 2006, 12:41
par Silver53 » 14 Oct 2006, 12:41
Quelqu'un saurait il m'aider svp?
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Oct 2006, 12:46
par abcd22 » 14 Oct 2006, 12:46
Pour Z1, on trouve
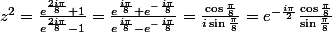
, et il faut réfléchir au signe de

pour trouver les 2 racines carrées.
Pour les autres valeurs de k tu fais exactement le même calcul jusqu'à la détermination des racines carrées, c'est pour ça que je suggérais de ne le faire qu'une fois en ne remplaçant pas k par une valeur. Pour k = 0 il n'y a pas de solution.
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Oct 2006, 12:47
par abcd22 » 14 Oct 2006, 12:47
Rq : quand on a des racines carrées de complexes à déterminer c'est beaucoup plus simple en écrivant les nombres sous forme exponentielle plutôt que sous forme algébrique.
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 14 Oct 2006, 16:20
par Silver53 » 14 Oct 2006, 16:20
abcd22 a écrit:Pour Z1, on trouve
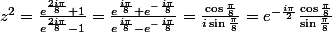
Peux tu m'expliquer ta simplification car je ne la retrouve pas. Notament ce p assage
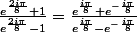
-
Silver53
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2006, 18:47
-
 par Silver53 » 14 Oct 2006, 17:30
par Silver53 » 14 Oct 2006, 17:30
ok j'ai enfin trouvée la simplification :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
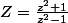 , pour trouver le module de
, pour trouver le module de  dois-je remplacer
dois-je remplacer  par
par ) ? puis ensuite simplifier
? puis ensuite simplifier  , et trouver son argument?
, et trouver son argument?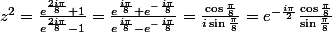 , et il faut réfléchir au signe de
, et il faut réfléchir au signe de  pour trouver les 2 racines carrées.
pour trouver les 2 racines carrées.