Enigme "LE CUBE"

[mind]

Bonjour,
Un ami m'a mis au défis de résoudre une énigme. N'étant pas très doué en math, j'aimerais que quelqu'un m'aide à comprendre le raisonnement. Je me perds dans les calculs alors qu'en soit ça doit être simple
Merci à ceux qui me répondront, bonne journée

Voici l'énoncé :
Un cube en bois a été peint tout en rouge. Ce cube a été découpé exactement et entièrement en petits cubes d'un centimètre d’arrête.
Une personne a remarqué qu'il y avait six fois plus de cubes peints sur une seule face que sur deux faces.
Quel était le volume initial du gros cube ?

[Imod]

Trop simple , 2 744 cm³ ( ou 8 cm³ si on manque de courage ) .

Imod

[mind]

Pourrais-tu m'expliquer ton raisonnement ?

[Imod]

Il suffit de compter en fonction de l'arête "x" , le nombre de cubes à une seule face rouge et le nombre de cubes à deux faces rouges puis écrire que le premier est six fois le deuxième .

Imod

[mind]

C'est au moment de la mise en équation, je ne sais pas poser les termes. Ce raisonnement je l'ai eu, mais pour le reste, comme je l'ai dit, pas très doué en math malheureusement

[siger]

bonjour

soit un grand cube comportant a petits cubes par arete

dans le grand cube il y a
8 sommets avec des petits cubes peints sur 3 faces: a eliminer
12 aretes comportant chacune (a-2) petits cubes peints sur 2 faces
6 faces comportant ( a-2)^2 petits cubes peints sur une face
....
6(a-2) ^2 = 6*(12 ( a-2))
soit (a-2) =12
....

[Imod]

Si

Imod

[mind]

Donc :
a-2=12
a = 10

une arete = 10 petits cubes
1 cube = 1cm donc une arete = 10 cm
Volume d'un cube = (arete)^3 = 10^3 = 1000 cm^3

est ce bon ?

[Imod]

10-2=12 ?

Imod

[mind]

6(a-2) ^2 = 6*(12 ( a-2))
simplifié => (a-2) =12
a = 12+2
a = 14 cubes par arête

Je pense avoir corrigé mon erreur

[Imod]

C'est ça , reste à traiter le cas un peu bizarre : a=2 .

Imod

[mind]

a=2 n'est pas possible
enfin je ne vois pas comment on pourrait faire (je parle de l'arete =2 cubes)

[mind]

Pourquoi chercher quand a=2 ?

[nodgim]

Quand a=2, ton équation est correcte car a-2 = 0
Cela dit, il y a 0 cube peint sur une seule face et 0 cube peint sur 2 faces, il n'y a que des cubes peints sur 3 faces.
Dans ce cas, le rapport entre les 2 types de cube est ce qu'on veut, et pourquoi pas 6.

[mind]

Pour l'énigme, si je dit :

6*(N-2)^2 = 6*(12( N-2))
simplifié => (N-2) =12
N = 12+2
N = 14 cubes par arête

Volume d'un cube = (N)^3
V(cube) = (N)^3 = (14)^3 = 2744 cm^3

J'ai bien répondu à son énigme non ? je ne pense pas que la solution soit si tordu que l'équation a-2=0. Qu'en pensez-vous ?

[Imod]

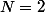
L'équation peut s'écrire et a deux solutions ou .

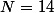
Imod

[mind]

Je vous remercie pour vos réponses. J'ai compris comment aborder le problème, c’était très instructif