Nombres complexes-interprétations géométriques

[jujudela]

Bonjour pourriez vous m'aider pour ces questions car je bloque totalement!!! (les interprétations géométriques, j'ai du mal!!!!!)


Le plan est rapporté à un repère orthonormal direct (O;u,v). On appelle f l'application qui, à tous points M d'affixe z (z différent de -1) associe le point M' d'affixe z' telle que:

z'=(-iz-2)/(z+1)

Soient A,B,C, les points d'affixes respectives a=-1, b=2i, c=-i.

4°)Pour tout nombre complexe z différent de -1, on considère le nombre
w=(z-2i)/(z+1).

a) Interpréter géométriquement l'argument du nombre complexe w.
b) Montrer que z'=-iw ( ca c'est fait!)
c) Déterminer l'ensemble (F) des points M d'affixe z telle que z' soit un imaginaire non nul.

MERCI BEAUCOUP

[Quidam]

Tout ça, c'est du cours !

La différence de l'affixe d'un point B et de celle d'un point A, c'est le complexe correspondant au vecteur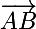
Le rapport du complexe correspondant à un vecteur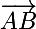 avec le complexe correspondant à un vecteur a pour module le rapport des normes des vecteurs, et pour argument l'angle des deux vecteurs ! Cela, tu es censé l'avoir appris en cours : il y en a pour quelques pages dans ton livre ! Je ne peux pas ici te refaire le cours : tu n'as qu'à relire (ou lire) ton cours !

w=(z-2i)/(z+1)
a=-1, b=2i, c=-i

Tu dois remarquer que (z-2i) représente le vecteur , que (z+1) représente le vecteur 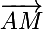et par conséquent que le rapport de ces deux quantités a pour argument l'angle

Une fois que tu auras compris ça, tu sauras faire ton exercice !