Il faudrait peut-être avoir un peu de bon sens (et aussi regarder la tête du résultat demandé).
Après avoir écrit que
^n=\big(n(1+\frac{a}{n})\big)^n)
il faut
évidement écrire que
\big)^n=n^n\big(1+\frac{a}{n}\big)^n)
vu que :
- Le
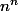
c'est un truc "extrêmement simple".
- Pour avoir un équivalent
d'un produit, il suffit d'avoir un équivalent de chaque terme du produit.
- Le
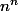
il apparait dans le résultat demandé.
- Le "reste", à savoir
^n)
est un truc super classique à évaluer.
Bref, il y a (au moins) 4 bonne raisons de poursuivre comme ça et pas comme tu l'a fait.
Et on peut même en donner une 5em qui rend le truc encore plus évident : pour montrer que deux trrucs sont équivalent, il faut montrer que le rapport tend vers 1 donc, ici, il faut montrer que
^n}{n^n\exp(a)})
tend vers 1 et là, ça "saute aux yeux" qu'il faut factoriser n au numérateur et le faire "sortir" de la parenthèse pour simplifier avec le
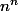
du bas.
