Décomposition de polynômes dans C[x]
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Donsalustre69 » 16 Nov 2016, 21:54
par Donsalustre69 » 16 Nov 2016, 21:54
Bonsoir,
Je suis en pleine remise à niveau de maths pour poursuivre des études d'ingénieur 3 ans après avoir quitté l'école et je révise actuellement la décomposition de polynômes et je bloque sur celui-ci:
 = x^{12}-1)
- 2 solution évidentes: x = 1 et x = -1 dans R[x]
- Ordre de multiplicité de la racine:
 = 0)
 = 11 \neq 0)
Donc
 = (x +1)(x -1)(ax^{2} + bx +c)^{5})
Pour trouver les coefficients, je fais la division euclidienne de P(x) par (x+1)(x-1) = x²-1
Je trouve comme quotient Q(x) =

, reste 0
Maintenant je suis censé faire quoi avec ça ? Est ce que je dois recommencer l'opération autant de fois que nécessaire pour décomposer ou y a t il une méthode plus rapide ?
Merci de votre aide.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 16 Nov 2016, 22:10
par XENSECP » 16 Nov 2016, 22:10
Salut,
Plus simplement tu cherches les racines réelles de l'unité.
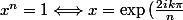})
avec

Du coup tu as bien trouvé k=0 et k=6.
Pas sûr qu'il y ait d'autres solutions réelles....
Sinon dans l'absolu avec ton Q(x), tu pouvais utiliser X=x² et trouver finalement X=-1 soit i et -i (soit k=3 et k=9). Ainsi tu avais 4 racines et tu pouvais encore avancer...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 22:23
par Ben314 » 16 Nov 2016, 22:23
Salut,
Je sais pas ce que tu as vu, mais si tu sait le faire, c'est le genre d'exo. où il faut quasi obligatoirement commencer par la décomposition dans C[X] pour en déduire
ensuite la décomposition dans R[X].
- C'est quoi les 12 racines
complexes de
\!=\!X^{12}\!-\!1)
(C est algébriquement clos, donc il y en a forcément 12 comptées avec leur ordre de multiplicité)
- C'est quoi la décomposition de P(X) dans

?
- Et dans
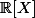
?
Sinon, ça :
Donsalustre69 a écrit:Donc
 = (x +1)(x -1)(ax^{2} + bx +c)^{5})
je sais pas d'où tu le sort, mais c'est complètement faux.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Izio38
- Messages: 8
- Enregistré le: 16 Nov 2016, 18:08
-
 par Izio38 » 16 Nov 2016, 23:11
par Izio38 » 16 Nov 2016, 23:11
Salut !
Je pense que chercher du côté du binôme de Newton pourrait t'aider


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2016, 23:24
par Ben314 » 16 Nov 2016, 23:24
Izio38 a écrit:Salut !
Je pense que chercher du côté du binôme de Newton pourrait t'aider

Hummmm.
J'ai de gros doutes.
Tu peut préciser où est-ce que tu compte utiliser la formule du binôme de Newton dans le contexte de l'exo. ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 17 Nov 2016, 07:37
par chan79 » 17 Nov 2016, 07:37
Donsalustre69 a écrit: = x^{12}-1)
- 2 solution évidentes: x = 1 et x = -1 dans R[x]
[/tex]
Pour trouver les coefficients, je fais la division euclidienne de P(x) par (x+1)(x-1) = x²-1
.
salut
Le mieux est de passer par les complexes.
=\prod_{k=0}^{11} (x-e^{\frac{k2i\pi}{12}))
Si tu veux décomposer dans

, tu multiplies certains facteurs entre eux.(dessine le cercle trigonométrique avec les racines douzième de 1 pour y voir plus clair).
Sinon, on peut y arriver avec les identités remarquables
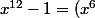^2-1^2=...)
à noter que

est divisible par

puisqu'il s'annule pour

et
Pourquoi ne pas le faire des deux façons ?
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 17 Nov 2016, 09:14
par Kolis » 17 Nov 2016, 09:14
Bonjour !
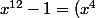^3-1=(x^4-1)((x^4)^2+x^4+1))
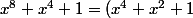(x^4-x^2+1))
:
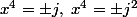
sont racines
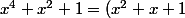(x^2-x+1))
: même démarche
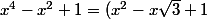(x^2+x\sqrt3+1))
:

sont racines et on les groupe par conjugaison...
Finalement :
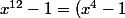(x^2+x+1)(x^2-x+1)(x^2-x\sqrt3+1)(x^2+x\sqrt3+1))

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 17 Nov 2016, 10:14
par chan79 » 17 Nov 2016, 10:14
salut
oui, on peut encore factoriser

 par Donsalustre69 » 17 Nov 2016, 19:06
par Donsalustre69 » 17 Nov 2016, 19:06
Merci a tous pour vos réponses,
Je constate qu'il existe plein de méthodes c'est plutôt pas mal ! J'ai essayé de calquer la méthode de résolution sur un exercice corrigé qui consistait à décomposer.

Racine évidente:
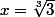
Donc:
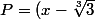(ax^{2} + bx +c))
On détermine les coeff a, b et c par division euclidienne de P par

On trouve:
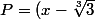(x^{2} + \sqrt[3]{3}x + \sqrt[3]{9}))
Ensuite on résoud
)
dans C[x]pour trouver les deux solutions complexes afin de décomposer ce dernier polynôme.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 17 Nov 2016, 20:04
par zygomatique » 17 Nov 2016, 20:04
salut
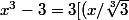^3 - 1])
et on cherche les racine cubique de l'unité ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
 par Donsalustre69 » 17 Nov 2016, 20:25
par Donsalustre69 » 17 Nov 2016, 20:25
Je ne connaissais pas cette définition, et le truc c'est qu'elle apparaît nulle part dans mes cours
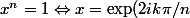)
J'ai cherché sur le net, polynômes cyclotomique. Je n'ai absolument jamais entendu parlé de ça... Je la garde sous le coude mais à mon avis le prof ne s'attend peut être pas à cette méthode.
Merci !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 18 Nov 2016, 14:37
par Carpate » 18 Nov 2016, 14:37
Donsalustre69 a écrit:Je ne connaissais pas cette définition, et le truc c'est qu'elle apparaît nulle part dans mes cours
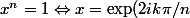)
Ce n'est pas une définition mais une équivalence qui s'établit en utilisant les propriéte bien connues des nombres complexes :
1 est sur l'axe des réels donc son argument est 0 modulo

, sa partie réelle est 1 et son module : 1
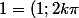 = e ^{2k\pi i})
si

,
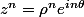
Inversement si
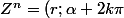)
,
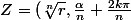=\sqrt[n]{r}.e^{i\frac{\alpha+2k\pi}{n}{)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
