Nombre de Mersenne [Spé maths]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
JeuneMatheux
- Membre Naturel
- Messages: 74
- Enregistré le: 13 Sep 2016, 20:11
-
 par JeuneMatheux » 14 Nov 2016, 21:36
par JeuneMatheux » 14 Nov 2016, 21:36
Bonjour, je n'arrive pas la question 2 et ça me bloque.
Voici l'énoncé :

Si vous m'expliquer en me disant qu'il faut faire la somme géométrique, j'aimerais comprendre pourquoi:)
Merci d'avance

"Ne t'inquiète pas si tu as des difficultés en maths, je peux t'assurer que les miennes sont bien plus importantes !" A.Einstein
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 14 Nov 2016, 22:05
par Pseuda » 14 Nov 2016, 22:05
Bonsoir,
Par la somme géométrique :
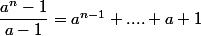
. Donc
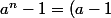(a^{n-1}+....+a+1))
.
Donc si
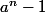
est premier, que peut-on en déduire pour
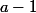
?
-
JeuneMatheux
- Membre Naturel
- Messages: 74
- Enregistré le: 13 Sep 2016, 20:11
-
 par JeuneMatheux » 14 Nov 2016, 22:23
par JeuneMatheux » 14 Nov 2016, 22:23
Je ne comprend pas ta déduction, comment après avoir trouvé la somme(chose que j'avais faites) peut on arriver a la déduction que
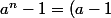(a^{n-1}+....+a+1))
?
Merci en tout cas

"Ne t'inquiète pas si tu as des difficultés en maths, je peux t'assurer que les miennes sont bien plus importantes !" A.Einstein
-
JeuneMatheux
- Membre Naturel
- Messages: 74
- Enregistré le: 13 Sep 2016, 20:11
-
 par JeuneMatheux » 14 Nov 2016, 22:23
par JeuneMatheux » 14 Nov 2016, 22:23
a si pardon en faites on isole a^n-1 désoler ^^ J'avais pas capté ^^
"Ne t'inquiète pas si tu as des difficultés en maths, je peux t'assurer que les miennes sont bien plus importantes !" A.Einstein
-
JeuneMatheux
- Membre Naturel
- Messages: 74
- Enregistré le: 13 Sep 2016, 20:11
-
 par JeuneMatheux » 14 Nov 2016, 22:33
par JeuneMatheux » 14 Nov 2016, 22:33
Cependant j'ai beau cherché je ne comprend pas ce que l'on peut en déduire

"Ne t'inquiète pas si tu as des difficultés en maths, je peux t'assurer que les miennes sont bien plus importantes !" A.Einstein

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 14 Nov 2016, 22:52
par Lostounet » 14 Nov 2016, 22:52
JeuneMatheux a écrit:Cependant j'ai beau cherché je ne comprend pas ce que l'on peut en déduire

Si tu as un nombre premier comme 17 la seule manière de l'écrire comme un produit d'entiers positifs ce serait par exemple 1*17 ou 17*1.
Donc si a^n-1 s'écrit comme un produit et qu'il est premier... tu dois avoir un des deux facteurs qui vaut 1 ! Lequel?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
JeuneMatheux
- Membre Naturel
- Messages: 74
- Enregistré le: 13 Sep 2016, 20:11
-
 par JeuneMatheux » 14 Nov 2016, 23:10
par JeuneMatheux » 14 Nov 2016, 23:10
Ah oui.... J'ai pas été très fute fute là ^^ Je partais trop loin, merci ducoup à vous deux

"Ne t'inquiète pas si tu as des difficultés en maths, je peux t'assurer que les miennes sont bien plus importantes !" A.Einstein
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités


