Svp aidez moi
6 messages
- Page 1 sur 1
Re: svp aidez moi
j avais distinguer deux cas
a=b
a différent de b et cette dernière se divise en deux sous cas
si a et b premier entre eux pgcd=1
si a et b ont un pgcd >1
et j avais trouver a=8 ou b=120
a=12 ou b = 20
a=20 ou b =12
a=120 ou b =8
seulement

 c qui m étonne qu il y d autre valeurs pour a et b comme a=30 b=10
c qui m étonne qu il y d autre valeurs pour a et b comme a=30 b=10
a=9 b=45
a=b
a différent de b et cette dernière se divise en deux sous cas
si a et b premier entre eux pgcd=1
si a et b ont un pgcd >1
et j avais trouver a=8 ou b=120
a=12 ou b = 20
a=20 ou b =12
a=120 ou b =8
seulement
a=9 b=45
Re: svp aidez moi
salut
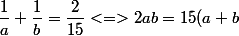) (1)
(1)
donc a et b ont même parité
écrivons a = 2p et b = 2q
alors (1) <=> ...
écrivons a = 2p + 1 et b = 2q + 1
donc (1) <=> ...
donc a et b ont même parité
écrivons a = 2p et b = 2q
alors (1) <=> ...
écrivons a = 2p + 1 et b = 2q + 1
donc (1) <=> ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: svp aidez moi
Salut,
Sinon, une autre méthode classique, mais qui demande un chouilla plus de bouteille, c'est la "mise sous forme canonique" :
\big(b\!-\!\frac{15}{2}\big)\!-\!\big(\frac{15}{2}\big)^2\Big]\!=\!0\ \Leftrightarrow\ (2a\!-\!15)(2b\!-15)\!=\!15^2)
Et il suffit alors de chercher tout les diviseurs de de façon à avoir toute les écritures de la forme
de façon à avoir toute les écritures de la forme 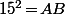 avec A et B entiers. (attention à ne pas oublier les diviseurs négatif, même si on ne cherche que les solutions avec a et b positif vu que 2a-15 peut être <0 même si a>0)
avec A et B entiers. (attention à ne pas oublier les diviseurs négatif, même si on ne cherche que les solutions avec a et b positif vu que 2a-15 peut être <0 même si a>0)
Sinon, une autre méthode classique, mais qui demande un chouilla plus de bouteille, c'est la "mise sous forme canonique" :
Et il suffit alors de chercher tout les diviseurs de
Modifié en dernier par Ben314 le 12 Nov 2016, 17:20, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: svp aidez moi
oui je voulais la proposer ensuite ... avec un chemin un chouia différent :
(2b - 15) = 15^2)

mais une recherche descendante est toujours instructive à traiter ...
mais une recherche descendante est toujours instructive à traiter ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
