Bonjour à tous!
Voici 3 jours que je patauge sur cette question, dans un DM de maths:
Nous avons (définies sur R), les fonctions f(x)= (7-2x)(x-1)² et g(x)=4x²-22x+28. La fonction g peut aussi s'écrire: g(x)=(4-2x)(7-2x). Il faut résoudre sur R l'équation f(x)=g(x).
J'ai tenté, dans un premier temps, de diviser les deux membres par 7-2x, mais mon prof de maths m'a dit que ce n'était pas possible (rapport au fait que si 7-2x= 0, la division par 0 est impossible).
Je bute donc sur cette petite question du DM... Pouvez-vous m'aider? Merci d'avance!
Résolution d'équation 2nde
8 messages
- Page 1 sur 1
Résolution d'équation 2nde
Une théorie mathématique ne doit être regardée comme parfaite que si elle a été rendue tellement claire qu’on peut la faire comprendre au premier individu rencontré dans la rue.
David Hilbert
David Hilbert
Re: Résolution d'équation 2nde
Tomli a écrit:Bonjour à tous!
Voici 3 jours que je patauge sur cette question, dans un DM de maths:
Nous avons (définies sur R), les fonctions f(x)= (7-2x)(x-1)² et g(x)=4x²-22x+28. La fonction g peut aussi s'écrire: g(x)=(4-2x)(7-2x). Il faut résoudre sur R l'équation f(x)=g(x).
J'ai tenté, dans un premier temps, de diviser les deux membres par 7-2x, mais mon prof de maths m'a dit que ce n'était pas possible (rapport au fait que si 7-2x= 0, la division par 0 est impossible).
Je bute donc sur cette petite question du DM... Pouvez-vous m'aider? Merci d'avance!
Bonjour,
Ca viendrait à dire que (7-2x)(x-1)² = (4-2x)(7-2x), non ? . . .
Donc à (x-1)² = (4-2x), non ? . . .
Re: Résolution d'équation 2nde
Oui, c'est ça!
Quand j'essaye de la résoudre, je tombe à un moment sur 2x^3, mais n'ayant vu en cours que des résolutions d'équations de premier et de seconde degré, ça me semble assez improbable...
Quand j'essaye de la résoudre, je tombe à un moment sur 2x^3, mais n'ayant vu en cours que des résolutions d'équations de premier et de seconde degré, ça me semble assez improbable...
Une théorie mathématique ne doit être regardée comme parfaite que si elle a été rendue tellement claire qu’on peut la faire comprendre au premier individu rencontré dans la rue.
David Hilbert
David Hilbert
Re: Résolution d'équation 2nde
Tomli a écrit:Oui, c'est ça!
Quand j'essaye de la résoudre, je tombe à un moment sur 2x^3, mais n'ayant vu en cours que des résolutions d'équations de premier et de seconde degré, ça me semble assez improbable...
(x-1)² = (4-2x) donne x² - 3 = 0 ou
Et comme on a simplifié auparavant (7-2x) on a aussi la 3è solution : 7-2x = 0 ===> x = . . . ?
que l'on peut observer ici :
Modifié en dernier par laetidom le 12 Nov 2016, 12:35, modifié 3 fois.
Re: Résolution d'équation 2nde
En fait, je ne sais pas si (x-1)² = (4-2x). J'étais arrivée à ce résultat en divisant par 7-2x, mais la méthode est apparemment mauvaise, même si les résultats semblent en concordance avec ceux attendus.
Je vais creuser cette piste, merci beaucoup!
Je vais creuser cette piste, merci beaucoup!
Une théorie mathématique ne doit être regardée comme parfaite que si elle a été rendue tellement claire qu’on peut la faire comprendre au premier individu rencontré dans la rue.
David Hilbert
David Hilbert
Re: Résolution d'équation 2nde
Tomli a écrit:En fait, je ne sais pas si (x-1)² = (4-2x). J'étais arrivée à ce résultat en divisant par 7-2x, mais la méthode est apparemment mauvaise, même si les résultats semblent en concordance avec ceux attendus.
Je vais creuser cette piste, merci beaucoup!
. . . oui effectivement, en simplifiant on a introduit que x soit différent de
Re: Résolution d'équation 2nde
Salut,
Donc si tu tient absolument à procéder de cette façon, ben il faut faire deux cas :
1) Si 7-2x est non nul alors, en divisant par 7-2x on obtient ...... et on trouve comme solution(s) x=......
2) Si 7-2x est nul alors ......
Et évidement que ce que tu trouve est cohérent avec le cas général vu que ça représente une des deux possibilités (celle où 7-2x est non nul). Par contre il risque éventuellement de te manquer une/des solution(s) vu que tu n'a pas traité tout les cas de figure possibles.
Et sinon, la façon "classique" de résoudre une équation (polynômiale) telle que (7-2x)(x-1)²=(4-2x)(7-2x), c'est :
(1) De retrancher des deux cotés le terme de droite (ou de gauche) donc écrire (7-2x)(x-1)²-(4-2x)(7-2x)=0
(2) De factoriser l'expression obtenue pour pouvoir utiliser le fait qu'un produit est nul ssi l'un des facteurs est nuls. Et ici, il y a un "facteur évident" qui est (7-2x) et l'équation se réécrit (7-2x)[(x-1)²-(4-2x)]=0 et on en déduit de nouveau qu'il faut que (x-1)²-(4-2x)=0 OU BIEN que 7-2x=0.
Le prof t'a pourtant parfaitement expliqué où se situait le problème : on ne peut diviser par 7-2x que si 7-2x est non nul.Tomli a écrit:En fait, je ne sais pas si (x-1)² = (4-2x). J'étais arrivée à ce résultat en divisant par 7-2x, mais la méthode est apparemment mauvaise, même si les résultats semblent en concordance avec ceux attendus.
Donc si tu tient absolument à procéder de cette façon, ben il faut faire deux cas :
1) Si 7-2x est non nul alors, en divisant par 7-2x on obtient ...... et on trouve comme solution(s) x=......
2) Si 7-2x est nul alors ......
Et évidement que ce que tu trouve est cohérent avec le cas général vu que ça représente une des deux possibilités (celle où 7-2x est non nul). Par contre il risque éventuellement de te manquer une/des solution(s) vu que tu n'a pas traité tout les cas de figure possibles.
Et sinon, la façon "classique" de résoudre une équation (polynômiale) telle que (7-2x)(x-1)²=(4-2x)(7-2x), c'est :
(1) De retrancher des deux cotés le terme de droite (ou de gauche) donc écrire (7-2x)(x-1)²-(4-2x)(7-2x)=0
(2) De factoriser l'expression obtenue pour pouvoir utiliser le fait qu'un produit est nul ssi l'un des facteurs est nuls. Et ici, il y a un "facteur évident" qui est (7-2x) et l'équation se réécrit (7-2x)[(x-1)²-(4-2x)]=0 et on en déduit de nouveau qu'il faut que (x-1)²-(4-2x)=0 OU BIEN que 7-2x=0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Résolution d'équation 2nde
et oui ! merci Ben ! par cette méthode (on ne rajoute pas de quotient et donc de dénominateur non nul comme contrainte) on a bien les trois solutions car on en déduit que :
[(x-1)^2 - (4-2x)] = 0)
(x^2 - 2x + 1 - 4 + 2x) = 0)
(x^2 - 3) = 0)
(x - \sqrt{3})(x + \sqrt{3}) = 0)
D'où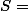 {
{ }
}
D'où
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
