Bonjour à tous,
Ayant un petit trou de mémoire pour la technique de résolution je sollicite votre aide.
Je me place dans le plan cartésien (O,x,y) et je veux simplement calculer l'intersection entre le cercle unité centré en (1,0) et la parabole d'équation y=x^2
Cela revient donc à résoudre le système suivant (sauf erreur de ma part) :
(x-1)^2 + y^2 =1
y = x^2
Ce système a à priori deux solutions dont le point (0,0) mais seulement je ne parviens pas à me ramener à une équation du second degré à un seul paramètre.
Si quelqu'un peut éclairer ma lanterne et me montrer la résolution ?
Merci d'avance !
Intersection parabole cercle
4 messages
- Page 1 sur 1
Re: Intersection parabole cercle
Ce système a à priori deux solutions dont le point (0,0) mais seulement je ne parviens pas à me ramener à une équation du second degré à un seul paramètre.
Bonjour,
L'égalité des deux équations donne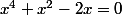
on peut factoriser par x ===>=0)
donc x=0 et une solution évidente pour le second terme avec x = 1
que l'on peut vérifier ici :
Bonjour,
L'égalité des deux équations donne
on peut factoriser par x ===>
donc x=0 et une solution évidente pour le second terme avec x = 1
que l'on peut vérifier ici :
Modifié en dernier par laetidom le 10 Nov 2016, 15:08, modifié 2 fois.
Re: Intersection parabole cercle
Je n'avais effectivement pas pensé à élever au carré la deuxième égalité avec d'effectuer la substitution.
Merci beaucoup !
Merci beaucoup !
Re: Intersection parabole cercle
Jig09 a écrit:Je n'avais effectivement pas pensé à élever au carré la deuxième égalité avec d'effectuer la substitution.
Merci beaucoup !
Content d'avoir aidé ! @+ sur le forum !
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
