Si on te demandais le volume (en cm^3) du verre complet (ou du demi verre), il te faudrait effectivement des valeurs numérique concernant la hauteur h du verre et le rayon R du cercle formant le haut du verre (qui est la base du cône...).
Mais ce n'est pas vraiment ça qu'on te demande. On te demande de déterminer quelle proportion
du volume du verre est rempli lorsque la hauteur du liquide atteint la moitié de la hauteur totale du verre.
Et une méthode pour trouver cette proportion (*) c'est de calculer le volume total du verre (on obtient une formule en fonction de h et de R bien sûr) puis de calculer le volume de liquide lorsque ce dernier atteint la mi-hauteur du verre (qui de nouveau est une une formule dépendant de h et de R). Enfin, tu doit faire la division de l'un par l'autre pour connaitre la proportion et dans ce dernier calcul, les R et les h vont se simplifier (ça me semble intuitivement évident, mais je sais pas si ça l'est forcément pour tout le monde).
Pour te donner le principe, pour le volume total du verre, la "base", c'est un disque de rayon R qui a donc une aire de
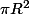
donc le volume complet du verre, c'est

Sur le premier dessin, la hauteur du cône représentant le liquide, c'est

, mais c'est quoi le rayon du cercle représentant la base du cône ?
(*) Il y a une autre méthode bien plus rapide utilisant les homothéties et la façon dont ces dernières modifient les longueurs, surfaces et les volumes, mais je sais pas si c'est connu au niveau Lycée...

