Equations cartésienne 1S

[GuillaumeS3]

Pour la 4.a) quand j'ai essayer les deux ça me donne pas les mêmes signes :

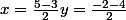
Du coup j'ai I=(1;-3) alors que quand je fais et que je divise par ça me donne alors que je devrais avoir les mêmes résultats non ?

[Dasson2]

(13/4; 3/4) c'est bien cela.
C'est même écrit dans http://rdassonval.free.fr/flash/for0411.jpg
Pour la 4a, pas de réponse car pas de question !

[GuillaumeS3]

(13/4; 3/4) c'est bien cela.
C'est même écrit dans http://rdassonval.free.fr/flash/for0411.jpg
Pour la 4a, pas de réponse car pas de question !

Dans la 4.a) on nous demande de calculer les coordonnées du milieu I du segment [BC]

[Dasson2]

Coordonnées du milieu d'un segment : demi-SOMME des abscisses des extrémités; demi-SOMME des ordonnées des extrémités.
Voir cours, vérifier en REGARDANT le dessin !
Confusions entre coordonnées d'un point et coordonnées d'un vecteur...

[GuillaumeS3]

Coordonnées du milieu d'un segment : demi-SOMME des abscisses des extrémités; demi-SOMME des ordonnées des extrémités.
Voir cours, vérifier en REGARDANT le dessin !
Confusions entre coordonnées d'un point et coordonnées d'un vecteur...

Ah je me suis tromper de signe...
Du coup c'est :

et
donc ?
En regardant quelle dessin ?

[Dasson2]

Placer les points dans un repère orthonormé avec papier crayon ou logiciel comme GeoGeBra...
C'est la première chose à faire.

[GuillaumeS3]

Placer les points dans un repère orthonormé avec papier crayon ou logiciel comme GeoGeBra...
C'est la première chose à faire.

J'ai vérifier en plaçant les points est effectivement
Merci ! pour le 4.b) je devrais réussir tout seul

[GuillaumeS3]

Salut,
Bon, ben c'est très très mal barré...
Déjà, calculer les coordonnées de MA² et MB², ça veut rien dire du tout vu que MA² et MB² c'est pas des points (ni des vecteurs) mais des réels.
Ensuite, pour déterminer les coordonnées des points A et B, vu le contexte, il est inutile (voire néfaste) de calculer les longueurs MA et MB.
Enfin, la formule que tu donne pour calculer les distances entre deux points ne s'applique pas dans le cas présent vu que le repère qu'on t'impose n'est pas orthonormé (la formule en question, c'est jamais qu'une réécriture du théorème de Pythagore donc il faut un angle droit et ce n'est pas le cas ici)

Pour trouver les coordonnées des différents points, ben il faut utilisiser la définition de ce que sont les coordonnées d'un point dans un repère.
Et cette définition est : "On dit qu'un point M a pour coordonnées (x,y) dans le repère lorsque ... "

Bonsoir ! je me suis attaquer à l'exercice 88 et pour les coordonnées de B et C j'ai trouver ça : B(0;15) et C(0;10) est ce juste ?
mais je ne sais pas comment trouver l'équations cartésiennes, j'ai essaye de la même manière que pour l'exercice précédant mais cela n'a pas marcher..