Les équations fonctionnelles

[Grizet]

Bonsoir, pour résoudre une équation fonctionnelle, il est logique d'utiliser la substitution.
Par exemple, je pourrais remplacer des inconnues par certaines valeurs pour obtenir des informations utiles et ainsi trouver au final les (la) solution(s) de l‘équation.

Toutefois, il arrive que certaines fonctions obtenues ne satisfont pas l'équation après vérification.
Comment cela se peut-il ?

Merci de votre aide.

[Ben314]

Salut,
Ca vient simplement du fait que, au départ, ton équation se présente sous la forme "pour tout x,y,... dans R on veut que ...." et que, lorsque tu remplace les inconnues par des valeurs, tu utilise ce qu'on appelle de façon pédante un "syllogisme" (le plus connu de tous étant "Tous les hommes sont mortels, or Socrate est un homme donc Socrate est mortel") qu'on résume parfois en disant "qui peut le plus peut le moins" (si c'est vrai pour tout les hommes, alors en particulier c'est vrai pour Socrate)
Or ce qu'il faut bien comprendre, c'est que ce raisonnement là (le syllogisme) n'est qu'une simple implication et surement pas une équivalence : Le fait que Socrate soit un homme mortel n'est clairement pas suffisant pour en déduire que tout les hommes sont mortels.
Donc en procédant de la sorte, tu perd de l'information par rapport à ce que tu avait au départ, et comme tu perd de l'information, ça augmente le nombre de solutions (moins tu as d'information concernant un truc donné, plus tu as de choix concernant ce qu'est le truc en question)

[Ben314]

Pour voir si tu comprend de quoi je parle, dis moi ce que tu pense de ça (et si tu vois le rapport avec ce dont je parle au dessus) :

On considère l'équation
En multipliant par les deux membres on obtient
On a donc c'est à dire soit et une solution "évidente" est .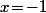
Sauf qu'en fait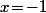 ne vérifie pas du tout l'équation de départ :
Pourquoi ?

[Grizet]

Bien que tu expliques bien, je ne suis pas sûr de comprendre, ni même l'exemple (que je te remercie d'avoir injecté dans réponse).
Je ne sais pas comment il faudrait faire pour que je comprenne ...

[Grizet]

Dans l'exemple, je crois que c'est parce que on a à faire à deux équation différentes P(x)=0 et x=0 qu'on fusionne ensemble, or les x ne valent pas forcément la meme chose (différent ensemble de solution(s) .

[Ben314]

Dans l'exemple, on a deux quantités, à savoir 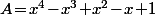et 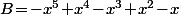qui sont toutes les deux nulles et on en a déduit qu'elle étaient égales.
On a donc utilisé le fait que, si A=0 et B=0 alors A=B.
Sauf qu'il est évident que ce n'est qu'une implication et pas une équivalence : si on sait uniquement que A=B, on ne risque pas d'en déduire que A=0 et B=0.
Par exemple, lorsque x=-1, on a A=5 et B=5 et on a effectivement A=B, mais on n'a pas A=0 et B=0.

Donc ce qu'il faut absolument maitriser, c'est, lorsque l'on fait une preuve, de savoir si on raisonne par équivalences ou par simple implication.
Si partant d'une égalité, on ajoute quelque chose aux deux membre, c'est une équivalence vu qu'il suffit de retrancher le même truc aux deux membres de la nouvelle équation pour retomber sur l'ancienne.
Lorsque l'on multiplie deux membres d'une égalité par la même chose, déjà, il faut faire plus attention : pour que ce soit une équivalence, il faut que le truc par lequel on multiplie soit non nul pour qu'on puisse diviser dans l'autre sens.
Par exemple, si x+5=2x-3 alors x(x+5)=x(2x-3) mais la réciproque, à savoir "si x(x+5)=x(2x-3) alors x+5=2x-3" n'est valable que si x est non nul. Et dans ce cas, on retrouve exactement le truc dont tu parle : l'équation "de départ" x+5=2x-3 a comme unique solution x=8 alors que l'équation "d'arrivé" x(x+5)=x(2x-3) a deux solutions x=8 et x=0. Le fait d'avoir procédé par implication et pas par équivalence fait qu'on a des solutions "en trop".
Et pour reprendre ton truc d'équation fonctionelle, le truc évident, c'est que partant de "pour tout x réel f(x)=g(x)", lorsque tu en déduit que (par exemple) f(0)=g(0), c'est une simple implication et surement pas une équivalence : il est clair que le simple fait que f(0)=g(0) ne signifie pas que f(x)=g(x) pour tout x.

Au Primaire/Lycée/Collège, on fait plus du tout de logique (chose que j'ai beaucoup de mal à comprendre : comment peut-on espérer apprendre aux élèves à raisonner sans logique...) mais il n'empêche que le fait est là : si tu raisonne par implication et pas par équivalence, ben tu risque fortement de trouver plus de solution que ce que le problème de départ en a et il faudra les vérifier.
De toute façon, ce qu'on peut se dire, c'est que dans le doute (je sais pas trop si j'ai raisonné par équivalence ou pas...), y'a qu'à vérifier.

[Grizet]

J'ai compris, enfin ! Merci de ton aide !


PS: c'est vrai que concernant les cours de logique, je n'en ai jamais eu ...