Bonjour
On a x1+x2+.............xn = 0
(Les 1,2....n sont les indices)
Comment resoudre ce systeme ?
J'ai utilisé la methode du pivot
En fixant x1 = t
On obtitent x2=-(t+x3+......+xn)
Mais je me suis arreter ici , je ne vois pas comment continuer ?
Merci d'avance
Exercice systeme lineaire (urgent)
5 messages
- Page 1 sur 1
Re: Exercice systeme lineaire (urgent)
Salut,
Si tu n'as effectivement qu'une seule telle équation et n inconnues alors c'est enfantin : il est évident que tu peut choisir totalement au pif la valeur n-1 des n variables puis choisir convenablement la valeur de la dernière variable (égale à l'opposée de la somme des autres) pour que la somme fasse zéro.
Si tu n'as effectivement qu'une seule telle équation et n inconnues alors c'est enfantin : il est évident que tu peut choisir totalement au pif la valeur n-1 des n variables puis choisir convenablement la valeur de la dernière variable (égale à l'opposée de la somme des autres) pour que la somme fasse zéro.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Exercice systeme lineaire (urgent)
Siger voila l'equation :
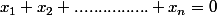
Ben314 execusez moi mais je n'ai pas bien compris : est qu'on peut affecter chaque inconnu a un parametre quelconque ?
D'apres ce que je connnais on choisit un inconnu qu'on fixe et ecris les autres en fonction de ce paramtre
On a
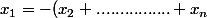)
et si on choisit par expl x_{1}=t
alors on obtiendra
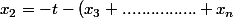)
Je ne vois pas ou avancez
Ben314 execusez moi mais je n'ai pas bien compris : est qu'on peut affecter chaque inconnu a un parametre quelconque ?
D'apres ce que je connnais on choisit un inconnu qu'on fixe et ecris les autres en fonction de ce paramtre
On a
et si on choisit par expl x_{1}=t
alors on obtiendra
Je ne vois pas ou avancez
Re: Exercice systeme lineaire (urgent)
Re
Lorsque l'on a un syteme de n equations linearaires independantes a m inconnues :
si m<n en general le systeme n'a pas de solution
si m=n on obtient une solution (toutes les inconnues sont determinées)
si m<n on obtient m solutions fonctions des n-m inconnues restantes
ici avec une equation et n inconnues on ne peut determiner qu'une inconnue x1 en fonction des n-1 restantes qui pourront toutes etre elles choisies au hasard ( x1 sera l'opposée de leur somme)
Lorsque l'on a un syteme de n equations linearaires independantes a m inconnues :
si m<n en general le systeme n'a pas de solution
si m=n on obtient une solution (toutes les inconnues sont determinées)
si m<n on obtient m solutions fonctions des n-m inconnues restantes
ici avec une equation et n inconnues on ne peut determiner qu'une inconnue x1 en fonction des n-1 restantes qui pourront toutes etre elles choisies au hasard ( x1 sera l'opposée de leur somme)
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
