bonsoir
j'ai un exercice je ne sais pas comment m'y prendre
aider moi svp
soit I=[a,b] avec a<b
montrez que tout élément x de I s'écrit sous la forme
x= α.a + (1-α).b avec 0≤ α ≥ 1
Notion de logique
4 messages
- Page 1 sur 1
Re: notion de logique
Bonjour,
Résous l'équation d'inconnue par équivalence. Tu dois ensuite démontrer que le
par équivalence. Tu dois ensuite démontrer que le  trouvé vérifie :
trouvé vérifie : 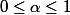
Résous l'équation d'inconnue
Re: notion de logique
Salut !
En fait, tu cherches à montrer que :
b\ ;\ t\in[0,1] \})
(j'ai pris au lieu de
au lieu de  pour bien distinguer les bornes de l'intervalle du réel compris entre
pour bien distinguer les bornes de l'intervalle du réel compris entre  et
et  .)
.)
Quelques observations géométriques :
- Si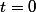 ,
, b=b) ; donc à
; donc à 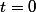 , on est situé à la borne
, on est situé à la borne  .
.
- Si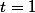 ,
, b=a) ; donc à
; donc à 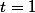 , on est situé à l'autre borne
, on est situé à l'autre borne  .
.
- Si ,
, b=\frac{1}{2}(a+b)) , on est situé au milieu de l'intervalle
, on est situé au milieu de l'intervalle  .
.
- Si alors
alors b < ta + (1-t)b \le b) .
.
Si je pose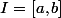 et
et b\ ;\ t\in[0,1] \}) , il faut donc montrer que
, il faut donc montrer que 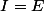 .
.
Pour montrer cette égalité, c'est toujours pareil, on montre que :
1) ;
;
2) .
.
Or pour montrer une inclusion du style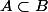 , il suffit de prendre un élément quelconque
, il suffit de prendre un élément quelconque 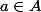 , et de montrer que
, et de montrer que 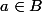 .
.
Parmi les deux inclusions 1) et 2), on peut déjà remarquer qu'il y en a une plus simple à montrer que l'autre. Laquelle ? Et pourquoi ?
En fait, tu cherches à montrer que :
(j'ai pris
Quelques observations géométriques :
- Si
- Si
- Si
- Si
Si je pose
Pour montrer cette égalité, c'est toujours pareil, on montre que :
1)
2)
Or pour montrer une inclusion du style
Parmi les deux inclusions 1) et 2), on peut déjà remarquer qu'il y en a une plus simple à montrer que l'autre. Laquelle ? Et pourquoi ?
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
