Équation de ce Cône !

[mari5029]

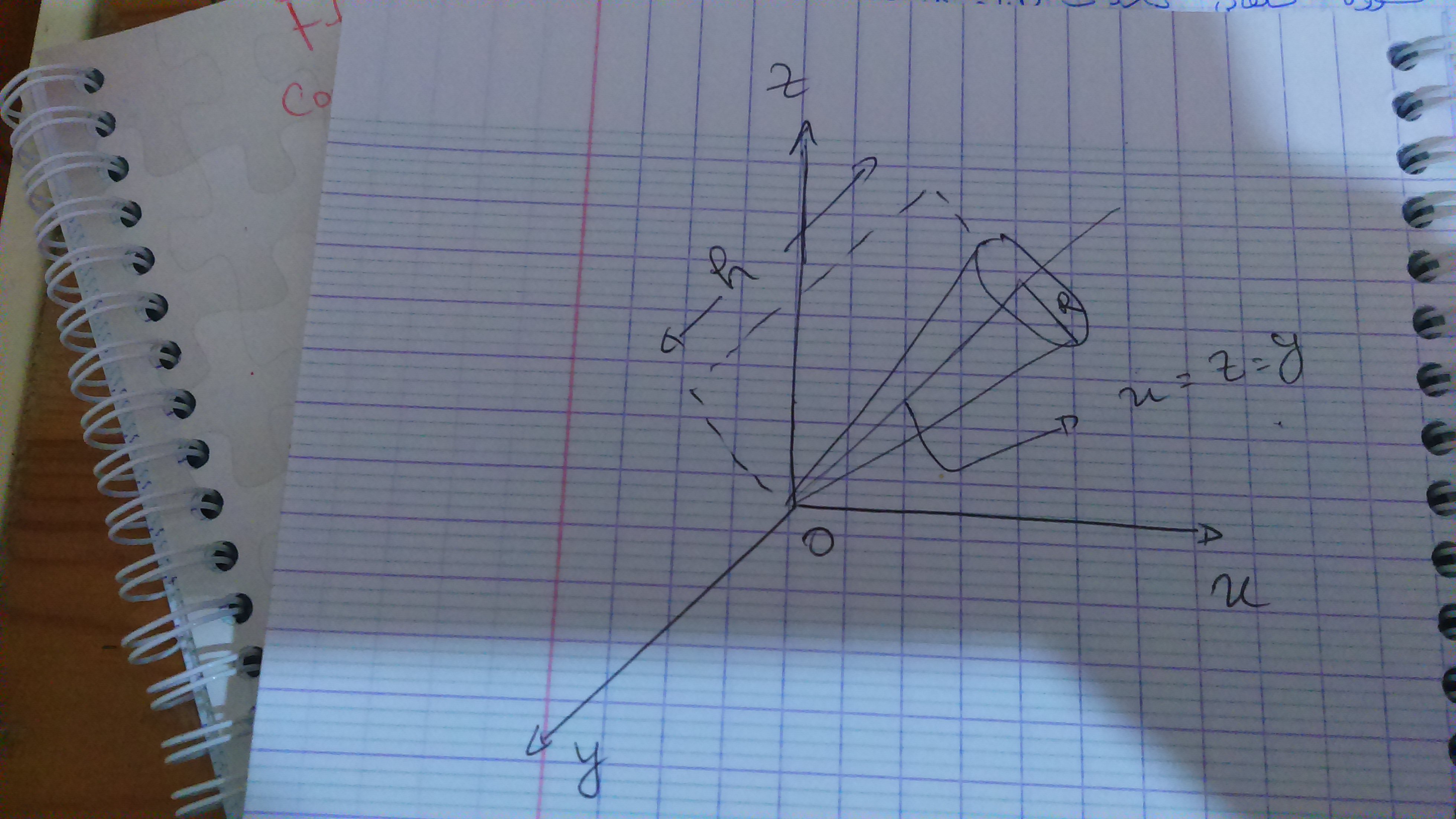
Pouvez-vous m'aider à trouver l'équation de ce Cône ? Je galère depuis une bonne heure.

Énoncé de l'exercice :

R: rayon
h: hauteur
Sommet du cône ô(0,0)
Trissectrice droite: X=y=z
N (vecteur) / S 1/ racine carrée (3). (1,1,1) vecteur unitaire normale aux sections du cône.

Question: déterminez l'équation du cône ?

[Ben314]

Salut,
1) Si M est un point de l'espace et P son projeté orthogonal sur la droite x=y=z, alors M est sur le cône complet (i.e. infini des deux cotés de O) ssi OP/PM=h/R (Thalès).
2) Si M:(x,y,z) alors P:(t,t,t) et on doit avoir vecteur(MP) orthogonal à (1,1,1) ce qui conduit à t=(x+y+z)/3.
Il n'y a plus qu'à écrire R²OP²=h²PM² pour avoir l'équation quadratique du cône complet.
3) Concernant la "portion de cône" de ton dessin, il suffit bien évidement de rajouter les inégalités 0<=x+y+z<=h/racine(3) pour signaler qu'on ne prend que la "bande" comprise entre les plans x+y+z=0 et x+y+z=h/racine(3).

Edit : vu que le centre du cône est en O:(0,0,0), il y a légèrement moins de calcul en prenant comme équation "caractéristique" OP/OM=h/racine(h²+R²) mais ça ne change évidement rien...