Valeur absolue \sqrt

[user080375]

Bonjour voilà mon résultat à la résolution d'inéquation avec valeur absolue :





ou




La solution de l'inéquation est S = .

[user080375]

Svp, j'ai besoin de savoir si j'ai juste ou pas..

[zygomatique]

salut

c'est bon mais c'est très al rédigé ...

en particulier ce n'est pas "la solution de ... est ..." mais "l'ensemble des solutions de ... est ..."

[user080375]

Lol "très al rédigé". C'est vrai que vous vous en sortez bien en orthographe vous. Mais merci quand même.

[Carpate]

Je verrais plutôt une explicitation de la levée de la valeur absolue (elle permet d'écarter la valeur -2 de la solution) :
a) x + 2 < 0 soit x < -2
|x+2| = -(x+2)
etc

b) x + 2 >0 soit x > -2
|x+2| = x + 2
etc

c) x = -2 pas de solution

[chan79]

salut
on pourrait écrire
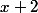
a une valeur absolue plus grande que s'il est lui-même plus grand que ou bien inférieur à .
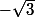
L'ensemble des solutions est bien la réunion des deux intervalles trouvés.

[user080375]

Merci bcp.

[zygomatique]

Lol "très al rédigé". C'est vrai que vous vous en sortez bien en orthographe vous. Mais merci quand même.

MDR

tu n'as jamais oublié une lettre en tapant sur ordinateur ...

ce n'est pas la justification de la disparition de la valeur absolue c'est simplement soit de travailler par équivalence propre (ce qui n’apparaît pas ici) soit prouver que ce qu'on a trouvé marche ...

mais surtout si a >= 0 ce qu'il faut respecter c'est l'équivalence : OU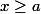

donc ici (en omettant éventuellement le signe d'équivalence <=> suivant le niveau) il faut le rédigé ainsi :





puis la réponse ...

[beagle]

Je ne comprends pas trop pourquoi "la solution est l'ensemble S"
doit impérativement se transformer en l'ensemble des solutions est l'ensemble S

Si l'ensemble S est l'unique solution , alors c'est La solution ...

Encore un effet du vivre ensemble!

[zygomatique]

S est un ensemble de nombres qui sont les solutions

une solution de cette équation est un nombre ... pas un ensemble ...

[beagle]

Bonjour zygomatique,
le soucis c'est que tu fais un usage propriétaire du terme solution dans cette affaire.

En mathématiques on utilise également solution pour j'ai un énoncé de problème pour lequel je cherche la solution.Donc ici, résoudre l'inéquation, c'est chercher tous les x qui ..., on cherche l'ensemble des x .
Donc il est bien normal que la solution au problème de résolution de l'inéquation soit un ensemble.
La phrase de user* est bien la solution (au problème posé) est l'ensemble S =...
C'est tout à fait correct.

Bon , beaucoup plus intéressant est la discussion sur comment on traduit l'équivalence ... ou ...
nous sommes d'accord.