Barycentre

par **nath59320** » 07 Oct 2006, 12:50

bonjours a tous,petit probleme sur un exo sur les barycentre est ce que qqun peut m'aider svp merci.

1)prouver qu'un quadrilatere ABCD est un parellelogramme si et seulement si D est le barycentre du systeme (A,1)(C;1)(B;-1)
2)application;soient ABCD et A'B'C'D' deux parallelogramme,soient I,J,K,L les point milieux respectifs de (AA') . (BB') (CC') (DD').Prouver que IJKL est un parallelogramme ,puis que le centre de IJKL est le milieu des centre de ABCD et A'B'C'D'..

merci bcp...
.

par **Zebulon** » 07 Oct 2006, 12:57

Bonjour,
commencez par :
D est le barycentre de {(A,1),(B,-1),(C,1)} si et seulement si

.
Est-il vrai que

si et seulement si ABCD est un parallélogramme?
Partez de

et raisonnez par équivalence pour arriver à ABCD est un parallélogramme.

par **jiji59320** » 07 Oct 2006, 14:33

bonjours merci de m'avoir repondu mais je ne comprend pas votre raisonnement.
pouvez vous m'expliquer en detail svp.

par **jiji59320** » 08 Oct 2006, 09:18

svp vous ne pouver pas m'aider d'avantage svp merci d'avance.....

par **Zebulon** » 08 Oct 2006, 09:32

D barycentre de {(A,1),(B,-1),(C,1)}

jusque-là, ça va?
Or

. Utilisez ensuite la relation de Chasles.

par **jiji59320** » 08 Oct 2006, 12:05

rebonjours,excusez moi mais je ne comprend pas dutout comment vous faite pour savoir que -BD=BD.
pouvez vous m'aidez d'avanctage merci bien...

par **Zebulon** » 08 Oct 2006, 12:27

J'ai dit :

Zebulon a écrit:

et pas

jiji59320 a écrit:-BD=BD.

1). Il s'agit de vecteurs, donc on met une flèche dessus. Vous connaissez la différence entre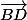

et BD?

2). La définition de

est :
c'est LE vecteur tel que, additionné avec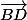

, ça fait

.
Pour montrer que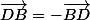

, il suffit donc de l'ajouter à

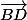et montrer que c'est égal à

, c'est-à-dire que

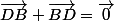. Or ceci est bien vrai d'après le relation de Chasles.
Je ne sais pas si vous avez bien compris la "preuve" que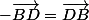

. Si oui, c'est très bien, sinon, ce n'est pas bien grave du moment que vous le savez.
Si vous ne l'avez pas comprise, il faut aussi savoir que c'est vrai pour n'importe quel vecteur.

par **jiji59320** » 08 Oct 2006, 12:45

ok j'avais compis ca je c aussi la difference entre vecteur ab et (ab).
mais ce que je ne comprend pas c'est comment on peut prouver grace a ce que vous dite que abcd est un parallelogramme...
meric d'avance

par **Zebulon** » 08 Oct 2006, 12:51

Simplifiez

à l'aide de la relation de Chasles.

par **jiji59320** » 09 Oct 2006, 17:47

rebonjours,voila j'ai simplifier grace a la relation de chales mais maintenant grace a cela comment je peux "prouver" comme on la demande dans l'enoncé que abcd est un parallelogramme.
merci par avance de votre aide.

par **Zebulon** » 09 Oct 2006, 17:48

Qu'est-ce que vous trouvez en simplifiant?

par **jiji59320** » 09 Oct 2006, 17:55

je ne c'est pas si cela est bon mais bon je vous donne mon resultat

vecteur AD= (vecteur BA)- (vecteur CA)

merci infiniment

par **Zebulon** » 09 Oct 2006, 18:00

Oui, c'est bon. Continuez votre calcul en changeant

en

.

par **jiji59320** » 09 Oct 2006, 21:45

bonsoir voila j'ai remplacer ce que vous m'avez dit et j'obtien donc

vecteur AD= vecteur BA+vecteur AC

PS ce qu'on est entrain de faire c'est la question 1 ?

meric de votre aide

par **Zebulon** » 10 Oct 2006, 05:49

Oui, on fait bien la question 1.

jiji59320 a écrit:vecteur AD= vecteur BA+vecteur AC

Qu'est-ce que ça donne en utilisant la relation de Chasles?

par **jiji59320** » 10 Oct 2006, 18:48

bonsoir apres la relation de chales j'obtien

vecteur AD = vecteur BC.

je crois que j'ai faux....

merci de votrz aide

par **Zebulon** » 11 Oct 2006, 14:56

jiji59320 a écrit:vecteur AD = vecteur BC.

Et ça, ça ne voudrait pas dire, par hasard, que ABCD est un parallélogramme?

par **jiji59320** » 11 Oct 2006, 15:00

AH oui merci beaucoup je suis bete je vien de le remarquer merci bcp.
ensuite a la question suivante par contre j'ai essayer en attendant votre reponse mais je ne trouve pas.²

par **jiji59320** » 11 Oct 2006, 17:33

j'ai essayer la question 2 encore une fois mais je ne trouve toujours pas pouvez vous me donner un petit coup de pouce merci d'avance

cordialement

par **jiji59320** » 12 Oct 2006, 09:58

bonjours,pouvez vous m'aider pour la question 2

meric infiniment