Dm maths spe
27 messages
- Page 1 sur 2 - 1, 2
 dm maths spe
dm maths spe
Bonjour j'ai un dm de spé maths a faire et je suis bloque c sur la divisibilité
Pour le premier exo c'est:
En rangeant n pièces de son puzzle, Claudia constate que:
Si elle les range par 5 il lui en reste 3
Si elle les range par 7 il lui en reste 2
Si elle les range par 9 il lui en reste 1
Si elle les range par 11 il ne lui en reste plus
Il faut déterminer le nombre de pièce sachant qu'il est inferieur a 2000 (le première question était de déterminer quatre diviseur premier de 2n-11)
J'ai compris mais je n'arrive pas a trouver la réponse ou du moins a expliquer un raisonnement convenable
Pour l'exo 2
On a Un= 2^3n-1 pour tout entier naturel n
J'ai déjà justifier que Un+1= 8Un+7
Mais il fait aussi démontrer que chaque Un est divisible par 7 est ce que quelqu'un peut m'explique comment on fait??
Merci d'avance
Pour le premier exo c'est:
En rangeant n pièces de son puzzle, Claudia constate que:
Si elle les range par 5 il lui en reste 3
Si elle les range par 7 il lui en reste 2
Si elle les range par 9 il lui en reste 1
Si elle les range par 11 il ne lui en reste plus
Il faut déterminer le nombre de pièce sachant qu'il est inferieur a 2000 (le première question était de déterminer quatre diviseur premier de 2n-11)
J'ai compris mais je n'arrive pas a trouver la réponse ou du moins a expliquer un raisonnement convenable
Pour l'exo 2
On a Un= 2^3n-1 pour tout entier naturel n
J'ai déjà justifier que Un+1= 8Un+7
Mais il fait aussi démontrer que chaque Un est divisible par 7 est ce que quelqu'un peut m'explique comment on fait??
Merci d'avance
Re: dm maths spe
mamaco860 a écrit:On a Un= 2^3n-1 pour tout entier naturel n
J'ai déjà justifier que Un+1= 8Un+7
Mais il fait aussi démontrer que chaque Un est divisible par 7 est ce que quelqu'un peut m'explique comment on fait??
Merci d'avance
Par récurrence :
Initialisation : U1 = 7
Hérédité : Si U(n) divisible par 7 , U(n) = 7k
Et alors U(n+1) = 8U(n) + 7 = 8*7k + 7 = 7*(8k + 1) donc U(n+1) divisible par 7
Re: dm maths spe
salut
 + u_n)
une récurrence est donc triviale ...
une récurrence est donc triviale ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: dm maths spe
Bonjour,
Pour l'exercice 1, c'est une application du théorème des restes chinois (mais je doute fort qu'il ait été vu en terminale, sauf éventuellement des exemples en exercice).
Sinon ce problème utilise les congruences et le fait que 5,7,9 et 11 sont premiers entre eux deux à deux. Ça se fera certainement à coups de théorème de Bézout.
Commence par traduire l'énoncé en termes de congruences...
Pour l'exercice 1, c'est une application du théorème des restes chinois (mais je doute fort qu'il ait été vu en terminale, sauf éventuellement des exemples en exercice).
Sinon ce problème utilise les congruences et le fait que 5,7,9 et 11 sont premiers entre eux deux à deux. Ça se fera certainement à coups de théorème de Bézout.
Commence par traduire l'énoncé en termes de congruences...
Re: dm maths spe
Bonjour,
Quelle était la question avec 2n -11 ?
Soit n le nombre de pièces. Comment peut-on traduire "Si elle les range par 5 il lui en reste 3" en terme de divisibilité ? Et : "Si elle les range par 7 il lui en reste 2" ?
Dès lors, tu peux remarquer que 35 divise quoi ? ...... tu dois aboutir à 2n -11.
Quelle était la question avec 2n -11 ?
Soit n le nombre de pièces. Comment peut-on traduire "Si elle les range par 5 il lui en reste 3" en terme de divisibilité ? Et : "Si elle les range par 7 il lui en reste 2" ?
Dès lors, tu peux remarquer que 35 divise quoi ? ...... tu dois aboutir à 2n -11.
Re: dm maths spe
D'accord sauf que le problème je n'ai pas vu les congruences j'ai vu que le division euclidienne
Faut il pas se servir de la première question qui est de déterminer quatre diviseurs premiers de 2n-11 ??
J'ai répondu 3/5/7/11
Faut il pas se servir de la première question qui est de déterminer quatre diviseurs premiers de 2n-11 ??
J'ai répondu 3/5/7/11
Re: dm maths spe
Mais quel était n dans la 1ère question ?
Comment peut-on traduire "Si elle les range par 5 il lui en reste 3" en terme de divisibilité ? : je n'ai pas fait allusion à une congruence, uniquement à une divisibilité. Comment, quoi divise quoi ?
Si elle en avait eu 3 de moins ....
Tu peux aussi l'exprimer avec une division euclidienne.
Comment peut-on traduire "Si elle les range par 5 il lui en reste 3" en terme de divisibilité ? : je n'ai pas fait allusion à une congruence, uniquement à une divisibilité. Comment, quoi divise quoi ?
Si elle en avait eu 3 de moins ....
Tu peux aussi l'exprimer avec une division euclidienne.
Re: dm maths spe
On peut traduit elle les range par 5 il lui en reste 3:
n= 5*q+3 soit n le nombre de pièce et q le nombre de groupe de 5
Pareil pour 7 il lui reste 2: n=7*q+2
35 = 2*23-11 ???
n= 5*q+3 soit n le nombre de pièce et q le nombre de groupe de 5
Pareil pour 7 il lui reste 2: n=7*q+2
35 = 2*23-11 ???
Re: dm maths spe
D'où sort le 23 ? Att, ce n'est pas le même quotient (q) pour les 2 divisions.
Pour ne pas s'encombrer avec des lettres, n= 5q +3 peut s'écrire aussi avec une divisibilité : 5 divise ?
Puis, tu auras : 7 divise ?
Il faut ensuite trouver un diviseur commun à une combinaison linéaire d'expressions qui contiennent n.
Pour ne pas s'encombrer avec des lettres, n= 5q +3 peut s'écrire aussi avec une divisibilité : 5 divise ?
Puis, tu auras : 7 divise ?
Il faut ensuite trouver un diviseur commun à une combinaison linéaire d'expressions qui contiennent n.
Re: dm maths spe
Le 23 sort de 35+11=46 et 46/2=23
Oui q n'est le même nombre car les groupes ne sont pas pareil
5divise n et 7 aussi mais il reste des pièces a la fin
n-3/5 = n-2/7= n-1/9= n/11 c ca??
Oui q n'est le même nombre car les groupes ne sont pas pareil
5divise n et 7 aussi mais il reste des pièces a la fin
n-3/5 = n-2/7= n-1/9= n/11 c ca??
Re: dm maths spe
Bon on peut le faire aussi avec les divisions euclidiennes :
n = 5 p + 3
n = 7 q + 2
Multiplie chacune des lignes pour avoir un diviseur commun : 35, c'est-à-dire la 1ère par 7, et la 2ème par 5.
Puis soustrais les 2 lignes. Tu dois obtenir une division de 2n par 35 : la plus petite solution est bien 23 (en ne tenant compte que de ces 2 lignes).
Tu peux continuer ensuite avec les 2 autres lignes (rangement par 9 (ou 3 ?) et par 11).
n = 5 p + 3
n = 7 q + 2
Multiplie chacune des lignes pour avoir un diviseur commun : 35, c'est-à-dire la 1ère par 7, et la 2ème par 5.
Puis soustrais les 2 lignes. Tu dois obtenir une division de 2n par 35 : la plus petite solution est bien 23 (en ne tenant compte que de ces 2 lignes).
Tu peux continuer ensuite avec les 2 autres lignes (rangement par 9 (ou 3 ?) et par 11).
Re: dm maths spe
Je suis desoler mais j'ai du mal surtout ce qui me perturbe c que l'on fait avec 7 et 5 mais il y a aussi 9 et 11 il fait faire pareil??
Re: dm maths spe
Normalement tu dois avoir 4 équations et 5 inconnues (dont ton nombre) ceci te donnera plusieurs solutions et on doit choisir la plus petite des solutions.
Re: dm maths spe
posons n = 5.7.9.11.k + r avec 0 =< r < 5.7.9.11
n est multiple de 11 donc r € {0, 11, 22, ... , (5.7.9 - 1)11} = E
n = 5(7.9.11k} + r avec r - 3 multiple de 5
on élimine de E tous les éléments x tels que x - 3 n'est pas multiple de 5 et on obtient un nouvel ensemble E'
n = 7(5.9.11k) + r avec r € E' et r - 2 est multiple de 7
on élimine de E' tous les éléments x tels x - 2 n'est pas multiple de 7 et on obtient un nouvel ensemble E"
n = 9(5.7.11k) + r avec r € E" et r - 1 est multiple de 9
on élimine de de E" tous les éléments x tels que x - 1 n'est pas multiple de 9 et on obtient un nouvel ensemble F
dons F (et ce qu'on aurait pu faire dès le début) on ne conserve que les entiers r tels que n = 5.7.9.11k + r < 2000 <=> r < 2000 (car 5.7.9.11 > 2000 => k = 0)
n est multiple de 11 donc r € {0, 11, 22, ... , (5.7.9 - 1)11} = E
n = 5(7.9.11k} + r avec r - 3 multiple de 5
on élimine de E tous les éléments x tels que x - 3 n'est pas multiple de 5 et on obtient un nouvel ensemble E'
n = 7(5.9.11k) + r avec r € E' et r - 2 est multiple de 7
on élimine de E' tous les éléments x tels x - 2 n'est pas multiple de 7 et on obtient un nouvel ensemble E"
n = 9(5.7.11k) + r avec r € E" et r - 1 est multiple de 9
on élimine de de E" tous les éléments x tels que x - 1 n'est pas multiple de 9 et on obtient un nouvel ensemble F
dons F (et ce qu'on aurait pu faire dès le début) on ne conserve que les entiers r tels que n = 5.7.9.11k + r < 2000 <=> r < 2000 (car 5.7.9.11 > 2000 => k = 0)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: dm maths spe
Soit  le nombre recherché
le nombre recherché  , nous avons:
, nous avons:
 ;
;
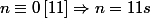 ;
; 
 car (
car (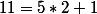 ), d’où:
), d’où:  (1);
(1); 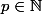
 car (
car (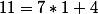 ), d’où:
), d’où:  (2);
(2); 
 car (
car (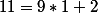 ), d’où:
), d’où:  (3);
(3); 
Élimine en utilisant les équations (2) et (3) que peut tu conclure? Essais de déterminer
en utilisant les équations (2) et (3) que peut tu conclure? Essais de déterminer  minimal.
minimal.
Élimine
Re: dm maths spe
bon il a sorti l'artillerie lourde .... 

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: dm maths spe
Sauf que ce doit juste avec la division euclidienne et la divisibilité et non avec les congruences car je ne l'ai pas fait
Re: dm maths spe
j'étais effectivement parti de 11 et fait des décompositions comme toi ....
on peut continuer une sorte de récurrence
n = 11s = 11(5p + 3)
s = 5p + 3 <=> 4s = 20p + 12
4s = 7r + 2
7r = 20p + 10 <=> p = 7(3p - r + 1) + 3 = 7k + 3
donc n = 11s = 11(5p + 3) = 55(7k + 3) + 33 = 5.7.11k + 198
...
on peut continuer une sorte de récurrence
n = 11s = 11(5p + 3)
s = 5p + 3 <=> 4s = 20p + 12
4s = 7r + 2
7r = 20p + 10 <=> p = 7(3p - r + 1) + 3 = 7k + 3
donc n = 11s = 11(5p + 3) = 55(7k + 3) + 33 = 5.7.11k + 198
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

