Équation (y-x)(y+x) = a
27 messages
- Page 1 sur 2 - 1, 2
Équation (y-x)(y+x) = a
Bonjour,
Je voudrais savoir comment résoudre ce type d'équation dans les réels positifs non nuls:
(y-x)(y+x) = a
Où x et y sont positifs
Merci
Je voudrais savoir comment résoudre ce type d'équation dans les réels positifs non nuls:
(y-x)(y+x) = a
Où x et y sont positifs
Merci
Re: Équation (y-x)(y+x) = a
Bonjour,
Comment faut il comprendre l'équation ?
Pour un "a" donné, déterminer un couple (x;y) ?
Est ce comme ça qu'il faut le comprendre ?
Comment faut il comprendre l'équation ?
Pour un "a" donné, déterminer un couple (x;y) ?
Est ce comme ça qu'il faut le comprendre ?
Re: Équation (y-x)(y+x) = a
Dans ce cas l'équation devient  donc
donc  et si
et si >0) alors l'ensemble des solutions est donné par
alors l'ensemble des solutions est donné par 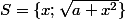
Re: Équation (y-x)(y+x) = a
C'est amusant car si "a" est un carré parfait alors "y" peut être vu comme l'hypothénuse d'un triangle 
Re: Équation (y-x)(y+x) = a
Cependant, si x et y sont inconnus et que seul a est connu, comment fait-on ?
Merci
Merci
Re: Équation (y-x)(y+x) = a
Vous fixez une valeur de x telle que (a+x^2)>0 et puis vous en déduisez la valeur de y
Re: Équation (y-x)(y+x) = a
Salut,
A mon avis, le truc qu'il faut bien comprendre, c'est que, autant les calculs d'Antony sont corrects, autant sa conclusion
L'ensemble des solution n'est absolument pas du tout constitué de deux réels :
- Déjà du fait que dans l'équation, il y a deux inconnues donc qu'une solution, c'est un couple de réels (et pas un réel) et qu'en conséquence, l'ensemble des solutions, c'est un ensemble de couples et pas un ensemble de réels.
- Ensuite (voire surtout) du fait que des couples de solutions, il y en a une infinité (et pas deux).
Donc si on tient absolument à parler de l'ensemble des solutions de l'équation, on peut par exemple écrire que c'est l'ensemble des couples de la forme) où
où  est un réel quelconque, ce qui, en écriture symbolique, s'écrit
est un réel quelconque, ce qui, en écriture symbolique, s'écrit 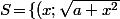\,:\,x\!\in\!{\mathbb R}\}) .
.
Et évidement, c'est extrêmement important de comprendre que, dans un cas pareil, il y a une infinité de solution vu que ça signifie qu'il est totalement hors de question de donner la liste complète de toute les solutions comme dans le cas des équation usuelles qu'on voit au Lycée.
Et si tu fait ce que dit Anthony, à savoir "choisir une valeur de x puis calculer le y correspondant", alors il est bien clair que tu ne répond plus à la question "Résoudre l'équation ...", mais à la question "Donner un exemple de solution de l'équation ....." ("résoudre" une équation, ça veut dire donner toutes les solutions de l'équation et pas uniquement une)
Pour te donner une analogie géométrique, ce type d'équation, c'est comme si on te demandais de déterminer quels sont les points M du plan qui sont à une distance de 3 d'un point A fixé.
La bonne réponse, c'est "Ce sont tout les points du cercles de centre A et de rayon 3" ce qui fait clairement une infinité de points. Et je pense que tu comprend que, si tu répond uniquement que tel point B situé à tel endroit est bien à une distance de 3 du point A, tu n'aura pas répondu à la question posée : tu aura juste donné un exemple de point solution du problème, mais pas tout les points solution du problème.
A mon avis, le truc qu'il faut bien comprendre, c'est que, autant les calculs d'Antony sont corrects, autant sa conclusion
est passablement fausse.anthony_unac a écrit:...
L'ensemble des solution n'est absolument pas du tout constitué de deux réels :
- Déjà du fait que dans l'équation, il y a deux inconnues donc qu'une solution, c'est un couple de réels (et pas un réel) et qu'en conséquence, l'ensemble des solutions, c'est un ensemble de couples et pas un ensemble de réels.
- Ensuite (voire surtout) du fait que des couples de solutions, il y en a une infinité (et pas deux).
Donc si on tient absolument à parler de l'ensemble des solutions de l'équation, on peut par exemple écrire que c'est l'ensemble des couples de la forme
Et évidement, c'est extrêmement important de comprendre que, dans un cas pareil, il y a une infinité de solution vu que ça signifie qu'il est totalement hors de question de donner la liste complète de toute les solutions comme dans le cas des équation usuelles qu'on voit au Lycée.
Et si tu fait ce que dit Anthony, à savoir "choisir une valeur de x puis calculer le y correspondant", alors il est bien clair que tu ne répond plus à la question "Résoudre l'équation ...", mais à la question "Donner un exemple de solution de l'équation ....." ("résoudre" une équation, ça veut dire donner toutes les solutions de l'équation et pas uniquement une)
Pour te donner une analogie géométrique, ce type d'équation, c'est comme si on te demandais de déterminer quels sont les points M du plan qui sont à une distance de 3 d'un point A fixé.
La bonne réponse, c'est "Ce sont tout les points du cercles de centre A et de rayon 3" ce qui fait clairement une infinité de points. Et je pense que tu comprend que, si tu répond uniquement que tel point B situé à tel endroit est bien à une distance de 3 du point A, tu n'aura pas répondu à la question posée : tu aura juste donné un exemple de point solution du problème, mais pas tout les points solution du problème.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Équation (y-x)(y+x) = a
Vous en pensez quoi tcdovdi14 ?
En gros ça va servir à quoi tout ça ?
C'est un problème physique à la base ou c'est purement mathématique ?
En gros ça va servir à quoi tout ça ?
C'est un problème physique à la base ou c'est purement mathématique ?
Re: Équation (y-x)(y+x) = a
Il est vrai que Ben314 n'a pas tord sur un point, le fait qu'il y est plusieurs couples possible sur ce genre d'équation. Mais la méthode d'anthony_unac n'est pas non plus fausse pour déterminer l'un à partir de l'autre.
A la base mon problème est purement mathématique. Après calculs de ma part sur le problème donné, je suis tombé sur:
y² - x² = 144 <=> (y - x)(y + x) = 144
et:
4y + 4x = 144 <=> y + x = 36
Sachant que y est strictement supérieur à x.
Je me suis donc mis à chercher un moyen de trouver x et y à partir de l'une des données, puis de l'autre et enfin des 2 en même temps. N'ayant pas trouvé au bout d'une heure, j'ai demandé à la communauté s'il y avait un moyen de résoudre une équation du type "(y - x)( y + x) = a" où toute les valeurs x, y et a sont strictement supérieure à 0.
Le problème est que je ne peux pas fixer x car justement, je le cherche tout comme y. Je ne connaît que a.
Merci de votre aide
PS: Sinon, est-il possible de passer de y² - x² = 144 à quelquechose du type y - x = ... ? En gros passer à une forme linéaire afin de facilité la résolution
A la base mon problème est purement mathématique. Après calculs de ma part sur le problème donné, je suis tombé sur:
y² - x² = 144 <=> (y - x)(y + x) = 144
et:
4y + 4x = 144 <=> y + x = 36
Sachant que y est strictement supérieur à x.
Je me suis donc mis à chercher un moyen de trouver x et y à partir de l'une des données, puis de l'autre et enfin des 2 en même temps. N'ayant pas trouvé au bout d'une heure, j'ai demandé à la communauté s'il y avait un moyen de résoudre une équation du type "(y - x)( y + x) = a" où toute les valeurs x, y et a sont strictement supérieure à 0.
Le problème est que je ne peux pas fixer x car justement, je le cherche tout comme y. Je ne connaît que a.
Merci de votre aide
PS: Sinon, est-il possible de passer de y² - x² = 144 à quelquechose du type y - x = ... ? En gros passer à une forme linéaire afin de facilité la résolution
Re: Équation (y-x)(y+x) = a
Vu la tête des équations, je me demande si tu ne nous aurait pas caché un "détail" concernant ls équations en questions, à savoir que, non seulement x et y doivent être positifs, mais aussi qu'ils doivent être entiers.
Et ce "détail", d'un point de vue mathématique, il est super archi hyper important : les méthodes que l'on emploie pour résoudre les "équations diophantiennes" (c'est à dire les équations dont on cherche les solutions entières) n'ont quasiment rien à voir avec les méthodes qu'on emploie pour résoudre les équations dans l'ensemble des nombres réels : LE outil de base pour les résolutions en nombre entiers, c'est la notion de divisibilité alors que dans R cette notion n'a absolument aucun intérêt vu que n'importe quel réel (non nul) divise n'importe quel autre réel.
Par exemple, si on cherche les solutions en nombre entiers positifs de (y-x)(y+x)=144, on les obtient très rapidement en dressant la liste des diviseurs entiers (positifs) de 144 (il n'y en a pas des tonnes et au final, on n'aura qu'un nombre fini de solutions).
Et ce "détail", d'un point de vue mathématique, il est super archi hyper important : les méthodes que l'on emploie pour résoudre les "équations diophantiennes" (c'est à dire les équations dont on cherche les solutions entières) n'ont quasiment rien à voir avec les méthodes qu'on emploie pour résoudre les équations dans l'ensemble des nombres réels : LE outil de base pour les résolutions en nombre entiers, c'est la notion de divisibilité alors que dans R cette notion n'a absolument aucun intérêt vu que n'importe quel réel (non nul) divise n'importe quel autre réel.
Par exemple, si on cherche les solutions en nombre entiers positifs de (y-x)(y+x)=144, on les obtient très rapidement en dressant la liste des diviseurs entiers (positifs) de 144 (il n'y en a pas des tonnes et au final, on n'aura qu'un nombre fini de solutions).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Équation (y-x)(y+x) = a
Voici l'énoncé:
Un potager est formé de 2 carrés. Il a fallu 144 m de bois pour entourer les deux carrés et l'on a semé de la pelouse sur les 144 m² de surface qui séparent les 2 carrés. Calculer les côtés de chaque carré.
Voici le schéma indiqué à côté de l'énoncé :
J'ai nomé x le côté du petit carré et y le côté du grand carré. Soit :

(y+x) = 144 = 12^{2})

Donc:


Car des longueurs sont forcement positives.
Je suis en train de calculer le reste...
Un potager est formé de 2 carrés. Il a fallu 144 m de bois pour entourer les deux carrés et l'on a semé de la pelouse sur les 144 m² de surface qui séparent les 2 carrés. Calculer les côtés de chaque carré.
Voici le schéma indiqué à côté de l'énoncé :
J'ai nomé x le côté du petit carré et y le côté du grand carré. Soit :
Donc:
Car des longueurs sont forcement positives.
Je suis en train de calculer le reste...
Re: Équation (y-x)(y+x) = a
Bonjour,
Vous pouvez facilement lister tous les couples solutions.
En partant de l'égalité , cela revient à chercher un triplet Pythagoricien
, cela revient à chercher un triplet Pythagoricien 
Vous pouvez facilement lister tous les couples solutions.
En partant de l'égalité
Re: Équation (y-x)(y+x) = a
tcdovdi14 a écrit:x = 12 et y = 24
A la louche 10*24=240>144 donc j'ai un doute sur cette solution

27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
