Bonsoir, j'essaie de finir un DM mais je bloque ici :
On appelle carré parfait, le carré d'un entier.
(a) Montrer que tout nombre premier impair est la différence de deux carrés parfaits.
(b) Vérifier que cette écriture est unique.
(c)Est-ce que tout nombre entier, pas forcément premier peut s'exprimer comme différence de deux carrés parfaits? Si oui, cette écriture est-elle unique?
Mes réponses:
(a) Je prend une la suite Un qui est la différence des carrés parfaits consécutifs ( pour tout n supérieur ou égal à 1) Un = n^2 -(n-1)^2 =2n-1
Ce qui me donne la suite des entiers impairs.
Donc tout entier impair peut s'écrire comme étant la différence de deux carrés parfaits, et ainsi tout nombre premier impair s'écrit comme la différence de deux carrés parfaits.
(b) Je vois pas comment faire là
(c) Là j'ai conjecturerais que non, j'arrive à construire tous les entiers impairs mais aussi la suite
Vn = n^2 - (n-2)^2
=4n-4
Qui me donne les multiples de 4, mais je dirais qu'on ne peut pas construire les entiers pairs multiples de 2.
Arithmétique L2
11 messages
- Page 1 sur 1
Re: Arithmétique L2
salut
un entier impair peut-il être la différence de deux carrés non consécutifs (différence des carrés de deux entiers consécutifs) ?
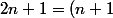^2 - n^2)
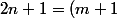^2 - m^2)
montre que m = n en soustrayant membre à membre...
c/ il suffit de prendre un contre exemple : 2 est-il la différence de deux carrés ....
 est multiple de 2
est multiple de 2
si p et q ont même parité alors est pair donc multiple de 2 (comme tout multiple de 4)
est pair donc multiple de 2 (comme tout multiple de 4)
par contre un multiple de 2 n'est pas toujours multiple de 4
...
un entier impair peut-il être la différence de deux carrés non consécutifs (différence des carrés de deux entiers consécutifs) ?
montre que m = n en soustrayant membre à membre...
c/ il suffit de prendre un contre exemple : 2 est-il la différence de deux carrés ....
si p et q ont même parité alors
par contre un multiple de 2 n'est pas toujours multiple de 4
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Arithmétique L2
Je suis pas sûr d'avoir bien compris :zygomatique a écrit:un entier impair peut-il être la différence de deux carrés non consécutifs (différence des carrés de deux entiers consécutifs) ?
105 = 54²-53² = 19²- 16² = 13²-8² = 11²-4²
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Arithmétique L2
Oui, 5^2-2^2= 21
et 11^2-10^2=21 aussi
Pour la b c'est donc un raisonnement par l'absurde que je dois écrire?
je suppose qu'il existe deux écriture l'une avec m l'autre avec n
et j'arrive à
2n+1=2m+1
n=m
donc absurde et unicité ?
pour la question c) je te suis mais je comprend pas pourquoi le contre exemple avec 2
et 11^2-10^2=21 aussi
Pour la b c'est donc un raisonnement par l'absurde que je dois écrire?
je suppose qu'il existe deux écriture l'une avec m l'autre avec n
et j'arrive à
2n+1=2m+1
n=m
donc absurde et unicité ?
pour la question c) je te suis mais je comprend pas pourquoi le contre exemple avec 2
Re: Arithmétique L2
Bonsoir,
Pour la b), tu peux utiliser l'identité remarquable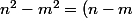(n+m)) . Si p premier =
. Si p premier = 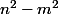 , que peux-tu dire de n et m ?
, que peux-tu dire de n et m ?
Pour la c), tu peux utiliser la même identité, et étudier les cas selon la parité de n et m.
Par exemple, 14 ne peut pas s'écrire comme la différence de 2 carrés parfaits.
Pour la b), tu peux utiliser l'identité remarquable
Pour la c), tu peux utiliser la même identité, et étudier les cas selon la parité de n et m.
Par exemple, 14 ne peut pas s'écrire comme la différence de 2 carrés parfaits.
Re: Arithmétique L2
si p est premier, (n-m) divise p ou (n+m) divise p
Je peux dire que n-m et n+m sont premiers entre eux?
si p^2-q^2 n'ont pas la même parité :
p=n+1 et q=n
p^2-q^2=2n+1
on peut alors construire tous les impairs
s'ils ont la même parité :
p=2+2 et q=n
p^2-q^2=4n+4
on peut alors construire tous les multiples de 4 (mais pas les multiples de 2)
ça suffit comme démonstration?
Je peux dire que n-m et n+m sont premiers entre eux?
si p^2-q^2 n'ont pas la même parité :
p=n+1 et q=n
p^2-q^2=2n+1
on peut alors construire tous les impairs
s'ils ont la même parité :
p=2+2 et q=n
p^2-q^2=4n+4
on peut alors construire tous les multiples de 4 (mais pas les multiples de 2)
ça suffit comme démonstration?
Re: Arithmétique L2
Ah, pour la b) je dirais :
Si p est premier, il n'admet que deux diviseurs, 1 et lui même, donc p=n^2-m^2=(n+m)(n-m)
donc n-m=1 et n+m=p est l'unique combinaison possible, c'est ça?
Si p est premier, il n'admet que deux diviseurs, 1 et lui même, donc p=n^2-m^2=(n+m)(n-m)
donc n-m=1 et n+m=p est l'unique combinaison possible, c'est ça?
Re: Arithmétique L2
Heu......
Je pense qu'il faudrait un minimum revoir le B-A-BA concernant la notion de divisibilité.
Lorsque tu écrit que p=(n-m)(n+m), alors, ce que ça implique (par définition même) que n-m divise p ET que n+m divise p (et jusque là, que p soit premier ou pas, ben ça change absolument rien à l'affaire !!!)
Ensuite, effectivement, les seuls diviseurs positifs d'un nombre premier p, c'est 1 et p mais les diviseurs "tout court", il y en a quatre : 1,-1,p et -p et des façons d'écrire p sous forme d'un produit, il y en a aussi 4 : p=1xp=px1=(-1)(-p)=(-p)x(-1).
Donc il y a un petit "quelque chose à dire" pour justifier que n-m=1 et que n+m=p (pourquoi pas n-m=p et n+m=1 ou bien n-m=-p et n+m=-1 ?)
Je pense qu'il faudrait un minimum revoir le B-A-BA concernant la notion de divisibilité.
Lorsque tu écrit que p=(n-m)(n+m), alors, ce que ça implique (par définition même) que n-m divise p ET que n+m divise p (et jusque là, que p soit premier ou pas, ben ça change absolument rien à l'affaire !!!)
Ensuite, effectivement, les seuls diviseurs positifs d'un nombre premier p, c'est 1 et p mais les diviseurs "tout court", il y en a quatre : 1,-1,p et -p et des façons d'écrire p sous forme d'un produit, il y en a aussi 4 : p=1xp=px1=(-1)(-p)=(-p)x(-1).
Donc il y a un petit "quelque chose à dire" pour justifier que n-m=1 et que n+m=p (pourquoi pas n-m=p et n+m=1 ou bien n-m=-p et n+m=-1 ?)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Arithmétique L2
Ah oui..
Pour la justification :
si n-m=p, alors n+m=1
si n-m=-p, alors n+m=-1
si n-m=-1, alors n+m=-p
si n-m=1, alors n+m=p
Pour la justification :
si n-m=p, alors n+m=1
si n-m=-p, alors n+m=-1
si n-m=-1, alors n+m=-p
si n-m=1, alors n+m=p
Re: Arithmétique L2
Thomas91 a écrit:Ah oui..
Pour la justification :
si n-m=p, alors n+m=1
si n-m=-p, alors n+m=-1
si n-m=-1, alors n+m=-p
si n-m=1, alors n+m=p
Bonjour,
On est bien d'accord là-dessus. Mais ceci ne justifie pas que la seule solution possible est : n-m=1 et n+m=p. D'où on en déduit (n,m) l'unique couple solution.
Re: Arithmétique L2
Ben314 a écrit:Je suis pas sûr d'avoir bien compris :zygomatique a écrit:un entier impair peut-il être la différence de deux carrés non consécutifs (différence des carrés de deux entiers consécutifs) ?
105 = 54²-53² = 19²- 16² = 13²-8² = 11²-4²
justement c'était pour demander pour l'unicité de l'écriture
on a évidemment
mais était-ce la seule ?
et tu viens de répondre que non ... par un exemple
mais pardon j'avions pas vu que dans la première question on parlait d'impair premier ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
