Inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mamo
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2016, 10:14
-
 par mamo » 16 Oct 2016, 10:26
par mamo » 16 Oct 2016, 10:26
Deuxième vrai / Faux que je ne réussi pas:
Pour tout entier naturel n strictement positif on a :

Pour moi cette affirmation est positive, j'ai testé avec les 3 premiers n et cela fonctionne maintenant je suis bloquée pour la démontrer...
Merci d'avance
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Oct 2016, 10:42
par chan79 » 16 Oct 2016, 10:42
Bonjour,
Indice: Quantité conjuguée
-
mamo
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2016, 10:14
-
 par mamo » 16 Oct 2016, 12:29
par mamo » 16 Oct 2016, 12:29
Il faut que je fasse la forme conjugué de celui du milieu? Car je ne comprend pas comment faire même avec la forme conjuguée que je maitrise bien pour les limites par exemple...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Oct 2016, 12:32
par chan79 » 16 Oct 2016, 12:32
oui
(a+b)}{a+b})
-
mamo
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2016, 10:14
-
 par mamo » 16 Oct 2016, 12:51
par mamo » 16 Oct 2016, 12:51
Je l'ai fait et j'obtient :

Mais après?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Oct 2016, 13:29
par Ben314 » 16 Oct 2016, 13:29
Salut,
Vu l'autre exo. que tu as posté, j'aurais tendance à me dire que c'est une planche d'exos sur le thème des accroissement finis donc que la réponse attendue serait plutôt celle utilisant ce théorème que celle proposée par chan79, mais bien sûr, rien ne t'empêche de faire les deux méthodes (toutes les deux extrêmement classiques donc à connaitre).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Oct 2016, 13:31
par Ben314 » 16 Oct 2016, 13:31
mamo a écrit:Je l'ai fait et j'obtient :

Mais après?
Ben aprés ça veut dire que l'inéquation de départ, tu peut la réécrire sous la forme

qui est équivalente à ....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mamo
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2016, 10:14
-
 par mamo » 16 Oct 2016, 14:09
par mamo » 16 Oct 2016, 14:09
Donc c'est équivalent à :
2

Mais je ne vois pas ou on veut en venir...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Oct 2016, 15:06
par Ben314 » 16 Oct 2016, 15:06
Bon, déjà, un petit rappel (de niveau collège...

), partant de a<b avec a et b de même signe, si on divise des deux cotés par le produit axb (qui est >0), on obtient 1/b<1/a ou, si tu préfère 1/a>1/b donc la "règle" c'est :
Si a et b sont de même signe (à ne pas oublier évidement...) et que a<b alors 1/a>1/b (et pas 1/a<1/b comme tu l'a écrit...)
Ensuite, ça :

c'est équivalent à quoi ?
et ça :

?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mamo
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2016, 10:14
-
 par mamo » 16 Oct 2016, 18:01
par mamo » 16 Oct 2016, 18:01
Oh oui milles excuses erreur de distraction je le sais en plus c'est logique...
Ensuite j'ai donc fait :
-> 2
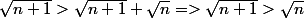
Ce qui est vrai puisque n > 0
-> 2
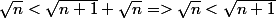
Ce qui est aussi vrai car n > 0
On a donc bien 2

D'où la propriété est vérifiée.
Merci beaucoup pour ton aide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
 ), partant de a<b avec a et b de même signe, si on divise des deux cotés par le produit axb (qui est >0), on obtient 1/b<1/a ou, si tu préfère 1/a>1/b donc la "règle" c'est :
), partant de a<b avec a et b de même signe, si on divise des deux cotés par le produit axb (qui est >0), on obtient 1/b<1/a ou, si tu préfère 1/a>1/b donc la "règle" c'est :