Bonjour a tous,
J'ai un dm de math normalement je nai jammais de mal mais la je bloque.
ABC est un triangle rectangle en A tel que AB=3, AC=4 et BC=5
M est un point du segment [BC]. Les perpendiculaires en M aux côtés [AB] et [AC] coupent ces côtés respectivement en P et N
Ou peut on placer le point M afin que la distance PN soit minimale?
ce que je sais est que APMN est un rectangle et dans un rectangle les diagonales ont la même longueur
donc AM = PN et si AM a une longueur minimale il en est de même de PN, et que AM est minimum lorsque AM perpendiculaire BC car AM=PN=2.4 ! mais comme je démontre que la longueur minimale de PN=2.4? je sais pour ça il faut trouvé la forme canonique? mais j'arrive pas je suis bloque
Merci, je serais reconnaissant de vous aide.
Plus court chemin (GÉOMÉTRIE PLANE)
8 messages
- Page 1 sur 1
Re: Plus court chemin (GÉOMÉTRIE PLANE)
Salut, personnellement je mettrais un plan car je préfère manipuler des coordonnées...
Re: Plus court chemin (GÉOMÉTRIE PLANE)
Ce que j'ai fait avec Geogebra, Mais moi j'ai pas vraiment manipulé les coordonnée en fait j'ai esseyez de prendre AN=y et AP=x aprés j'ai appliquer Thalès dans notre triangle ABC car (NM)//(AB) donc: CN/CA = CM/CB = NM/AB d'où: (4-y)/4 = x/3. En développant, on obtient: y= -4/3x+4.
De plus, j'ai appliquer Pythagore dans NAP, on a: PN= sqrt{y^2+x^2}.
Exprimons PN en fonction de x:
PN=f(x)=sqrt{(-4/3x+4)^2+x^2} et la je bloque, je ne suis pas sur si je suis sur le bon chemin ?
De plus, j'ai appliquer Pythagore dans NAP, on a: PN= sqrt{y^2+x^2}.
Exprimons PN en fonction de x:
PN=f(x)=sqrt{(-4/3x+4)^2+x^2} et la je bloque, je ne suis pas sur si je suis sur le bon chemin ?
- Fichiers joints
-
- Capture.JPG (54.75 Kio) Vu 1018 fois
Re: Plus court chemin (GÉOMÉTRIE PLANE)
Salut,
Je sais pas trop ce qui est attendu comme réponse :
Si l'énoncé est effectivement formulé sous la forme "où doit on placer le point M pour minimiser la distance PN", personnellement, j'aurais tendance à répondre "Il faut prendre pour M le projeté orthogonal de A sur le segment [BC]" qui répond bien à la question et qui permet de tracer (à la règle et au compas) très rapidement M sur une figure.
Mais on peut aussi considérer que le "où" de la question posée signifie en fait "à quelle distance de B" (ou de C).
Dans ce cas, pour trouver la distance en question, je pense que le plus simple est d'utiliser la proportionalité : les triangles (ABC) et (MBA) sont tout les deux rectangle [respectivement en A et en M] et l'angle en B de (ABC) est le même que l'angle en B de (MBA) donc les triangles sont semblables et les longueurs de leur cotés sont proportionnelles :
Je sais pas trop ce qui est attendu comme réponse :
Si l'énoncé est effectivement formulé sous la forme "où doit on placer le point M pour minimiser la distance PN", personnellement, j'aurais tendance à répondre "Il faut prendre pour M le projeté orthogonal de A sur le segment [BC]" qui répond bien à la question et qui permet de tracer (à la règle et au compas) très rapidement M sur une figure.
Mais on peut aussi considérer que le "où" de la question posée signifie en fait "à quelle distance de B" (ou de C).
Dans ce cas, pour trouver la distance en question, je pense que le plus simple est d'utiliser la proportionalité : les triangles (ABC) et (MBA) sont tout les deux rectangle [respectivement en A et en M] et l'angle en B de (ABC) est le même que l'angle en B de (MBA) donc les triangles sont semblables et les longueurs de leur cotés sont proportionnelles :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Plus court chemin (GÉOMÉTRIE PLANE)
salut
ou encore en calculant le double de l'aire de ABC de deux façons:
4*3=AM*5
ou encore en calculant le double de l'aire de ABC de deux façons:
4*3=AM*5
Re: Plus court chemin (GÉOMÉTRIE PLANE)
Et donc je trouve BM=1.8 et AM=2,4, OMG j'ai passé tout la journée a se faire galérer vous m’aviez sauvez, je suis nouvelle sur le site et je commence a vos aimez vraiment je vous aime trooooop! merci mille fois.
Re: Plus court chemin (GÉOMÉTRIE PLANE)
si on veut s'amuser en faisant compliqué :
on pose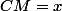
AL Kashi dans

Minimum pour x=3.2
et donc


à ne pas recopier !
on pose
AL Kashi dans
Minimum pour x=3.2
et donc
à ne pas recopier !

Re: Plus court chemin (GÉOMÉTRIE PLANE)
chan79 a écrit:si on veut s'amuser en faisant compliqué :
on pose
AL Kashi dans
Minimum pour x=3.2
et donc
à ne pas recopier !
tu es mon héro, et ne t’inquiète pas j'aime pas recopier des truc bêtement sans les comprendre, j'aimerais de les comprendre d'abord, puis d'être en mesure de les faire par moi-même .
 et merci encore une fois
et merci encore une fois
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
