égalité

[ldvalexander]

Pour un calcul de limite, je cherche à montrer cette égalité mais je m'embrouille avec toutes les racines. (j'ai bien compris qu'il fallait factoriser par la partie principale)

[samoufar]

Bonsoir,

D'abord, attention avec cette relation, elle n'est pas valable en 0.

Ensuite, pour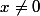 , il suffit de factoriser par en haut et en bas :

[ldvalexander]

merci mais je ne comprends pas bien la troisième égalité (après que tu es simplifié par sqrt(x) en haut et en bas)

[chan79]

Salut
J'élèverais ces deux membres positifs au carré, histoire de simplifier.
On s'en sort ensuite en factorisant .

[ldvalexander]

@ chan 79 je perds l'égalités en élevant au carrée. comment je fais pour savoir si je dois considérer sqrt(l) ou -sqrt(l) ? Et ça ne simplifie pas grand chose (j'ai juste plus à écrire les deux grosses racines)

@samoufar peux tu détailler la transition entre l'étape 2 et 3 merci

edit : si une fonction est positive sa limite est positive j'avais zappé autant pour moi chan

[chan79]

Deux nombres positifs sont égaux si leurs carrés sont égaux.

[ldvalexander]

ah oui, il y a donc équivalence. Mais dans ce qu'à fais samoufar je ne vois pas la transition entre les étapes 2 et 3. Peux tu m'aider car de toute façon même en élevant au carrée j'ai ce problème.

[Ben314]

Salut,
Si et sont deux réels positifs, alors .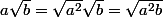
Et il applique ça avec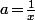 qui est bien un réel positif (sinon le tout "au fond" de ta formule ne voudrait rien dire)

[ldvalexander]

merci à tous j'ai enfin réussi à refaire le calcul ; je resserrais dans quelques jours