Terminale S Spé Math - Modulos

[Lowixx]

Bonjour,

J'ai cette question pour un DM : Démontrer que si le couple (x;y) est solution de (F) : 11x² - 7y² = 5 alors, x² congru 2y² [5].

Je pensais à dire : Si 11x² - 7y² = 5 alors 11x² - 7y² congru 0 [5] <=> 11x² congru 7x² [5]
or 11 congru 1 [5] et 7 congru 2 [5] donc x² congru 2y² [5]

Je ne sais pas si cette démarche est cohérente, qu'en pensez vous ?
Merci !

[zygomatique]

salut



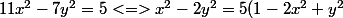et il suffit de moduler modulo 5 ....

[Lostounet]

Oui c'est cela.
Puisque 11 = 1(mod5)
Alors 11x^2=x^2 (mod 5)

7=2(mod 5)
7y^2=2y^2(mod 5)

Alors 11x^2+7y^2=x^2+2y^2 (mod 5)

Mais aussi 11x^2+7y^2=0 (5) par hypothèse

[Lowixx]

Ah merci ! Il fallait y penser.. J'aurais surement encore besoin d'aide plus tard !
Pour ce que me propose Lostounet, je comprend, mais comment j'explique que je passe de 11x^2+7y^2=x^2+2y^2 (mod 5) à x² = 2y² (mod 5) ?

[Lostounet]

Re
Bien entendu j'ai encore mal lu l'énoncé...

11x^2-7y^2=0 (5)

11x^2=x^2(5)
7y^2=2y^2 (5)

Du coup 11x^2-7y^2=x^2-2y^2(5)
Or ça vaut 0 par hypothèse

Donc..

[Lowixx]

Du coup 11x^2-7y^2=x^2-2y^2(5)
Or ça vaut 0 par hypothèse

Donc x^2-2y^2 = 0 (5), et de là, j'ai le droit de faire : x^2 = 2y^2 (5) ?

[Lostounet]

On a pas le droit d'ajouter le même nombre dans les modulos?

[Lowixx]

Je n'en étais pas sur mais je penses que oui. Donc x^2-2y^2 = 0 (5) <=> x^2-2y^2+2y^2 = 0+2y^2 (5) <=> x^2 = 2y^2 (5) tout simplement ?