Polynômes 2nd degrés
16 messages
- Page 1 sur 1
 Polynômes 2nd degrés
Polynômes 2nd degrés
Bonjour pouvez vous m'aidez svp
Démontrez qu'il existe un unique polygones P de degrés 2 tel que P(0)=0 et tel que pour tout réel x:
P(x)-P(x-1)=x
Démontrez qu'il existe un unique polygones P de degrés 2 tel que P(0)=0 et tel que pour tout réel x:
P(x)-P(x-1)=x
Re: Polynômes 2nd degrés
Aloha,
Pose P(x) = ax² + bx + c.
Tu cherches à trouver a,b et c.
Que t'impose la condition P(0)=0 ? Et P(x) - P(x-1) = 0 ?
Pose P(x) = ax² + bx + c.
Tu cherches à trouver a,b et c.
Que t'impose la condition P(0)=0 ? Et P(x) - P(x-1) = 0 ?
« Je ne suis pas un numéro, je suis un homme libre ! »
Re: Polynômes 2nd degrés
Que t'impose la condition P(0)=0 ? Et P(x) - P(x-1) = 0 ?[/quote]
Bonjour , merci de m'aidé mais j'ai cherché et je ne comprend pas ce que vous voulez dire
mais cela m'impose que le résultat sera toujours 0
Bonjour , merci de m'aidé mais j'ai cherché et je ne comprend pas ce que vous voulez dire
mais cela m'impose que le résultat sera toujours 0
Re: Polynômes 2nd degrés
Si  = ax^2+bx+c) alors
alors  = a \times 0^2 + b \times 0 + c = c) .
.
Or P(0) = 0 soit c = 0.
Du coup = ax^2+bx)
Ensuite calcule-P(x-1)) ce qui devrait te donner quelque chose comme
ce qui devrait te donner quelque chose comme 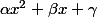 que tu devrais identifier avec la valeur de
que tu devrais identifier avec la valeur de  - P(x-1)) soit x ce qui impliquera un système d'équations:
soit x ce qui impliquera un système d'équations:

Allez finis tout seul maintenant !
Or P(0) = 0 soit c = 0.
Du coup
Ensuite calcule
Allez finis tout seul maintenant !
Re: Polynômes 2nd degrés
XENSECP a écrit:Sialors
.
Or P(0) = 0 soit c = 0.
Du coup
Ensuite calculece qui devrait te donner quelque chose comme
que tu devrais identifier avec la valeur de
soit x ce qui impliquera un système d'équations:
Allez finis tout seul maintenant !
merci mais je n'ai pas encore vue avec gamma et beta
Je trouve 2ax-a+b-x=0
Re: Polynômes 2nd degrés
Oui je suis d'accord que -P(x-1) = 2ax + (b-a))
Du coup on a bien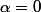 comme indiqué mais on s'en fiche.
comme indiqué mais on s'en fiche.
Puis si on continue l'identification des paramètres du polynome:
 ce qui te permet de trouver a et b, et c'est fini
ce qui te permet de trouver a et b, et c'est fini 
Du coup on a bien
Puis si on continue l'identification des paramètres du polynome:
Re: Polynômes 2nd degrés
moi j'ai continué en fessant une équation a double inconnue et j'ai trouvé a=5/9 et b=1/3
mais je pense que c'est faux , comment faut il faire ?
b=a
a=1/2 et b=1/2 également non ?

mais je pense que c'est faux , comment faut il faire ?
b=a
a=1/2 et b=1/2 également non ?
Re: Polynômes 2nd degrés
Je vois pas comment tu as pu trouver ce que tu as trouvé mais c'est vraiment plus simple que tu crois.
Du coup tu as d'un côté = P(x) - P(x-1) = 2ax - a + b)
De l'autre tu as = x)
Les coefficients de G sont: 2a et (b-a). Ceux de D sont 1 et 0.
Franchement je peux pas faire plus clair...
dans tes cours a écrit:2 polynomes sont égaux si leur degré est le même et leur coefficients terme à terme sont identiques
Du coup tu as d'un côté
De l'autre tu as
Les coefficients de G sont: 2a et (b-a). Ceux de D sont 1 et 0.
Franchement je peux pas faire plus clair...
Re: Polynômes 2nd degrés
bonsoir
il suffit de verifier que P(x) = 1/2(x²+x) repond aux conditions posées ........
TOTO0205 a écrit:Ce n'est pas 1/2 ?
il suffit de verifier que P(x) = 1/2(x²+x) repond aux conditions posées ........
Re: Polynômes 2nd degrés
siger a écrit:bonsoirTOTO0205 a écrit:Ce n'est pas 1/2 ?
il suffit de verifier que P(x) = 1/2(x²+x) repond aux conditions posées ........
Bonjour,
Sauf que je ne connais pas x
Re: Polynômes 2nd degrés
re
tu le fais exprès ou quoi?
en quoi as-tu besoin de x pour verifier P(x)-P(x-1)=x
c'est a dire
x²2/+x/2 -((x-1)²/2+(x-1)/2-x = 0 ?
et
P(0)=0 ?
tu le fais exprès ou quoi?
en quoi as-tu besoin de x pour verifier P(x)-P(x-1)=x
c'est a dire
x²2/+x/2 -((x-1)²/2+(x-1)/2-x = 0 ?
et
P(0)=0 ?
Re: Polynômes 2nd degrés
TOTO0205 a écrit:
Bonjour,
Sauf que je ne connais pas x
Bonsoir,
On n'a pas besoin de connaître "x". Autrement dit, "x" peut être n'importe quelle valeur. On cherche une relation qui marche pour n'importe quel "x". Et on l'appelle ..... x ..... justement. On aurait pu l'appeler "y", ou "z".
Mais pas "a", car ce qu'on cherche (les inconnues), c'est "a", "b" et "c", les coefficients du polynôme P(x)= ax²+ bx+ c.
Autrement dit, il faut que la relation : P(x) - P(x-1) = x, soit vraie pour tout x. Et on cherche a, b et c pour ça soit vrai.
Re: Polynômes 2nd degrés
siger a écrit:re
tu le fais exprès ou quoi?
en quoi as-tu besoin de x pour verifier P(x)-P(x-1)=x
c'est a dire
x²2/+x/2 -((x-1)²/2+(x-1)/2-x = 0 ?
et
P(0)=0 ?
je ne vois pas comment vous arrivez a mettre des carrés
Re: Polynômes 2nd degrés
Tu peux écrire x^2 pour x au carré au pire, on peut comprendre.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Polynômes 2nd degrés
Lostounet a écrit:Tu peux écrire x^2 pour x au carré au pire, on peut comprendre.
Jure?? Fou un peu non?
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
