Vérification réciproque bijection

[Tayyyy]

Bonjour,
je poste un message pour savoir si je me trompe totalement ou si le site où je dois faire mon dm bug.
Voici l'exercice :

f:[5,25]→[−124.64,−23.2]

f(x)=−5x+9/x.

Vérifiez que f est bijective, et calculez la fonction réciproque f^(−1):[−124.64,−23.2]→[5,25].

Pour la réciproque, je réponds :

f^(−1)(x) = 9/(x+5)

et on me dit : mauvaise réponse, la bonne réponse est: f^(-1)(x) = (x-sqrt(x^2+180))/(-10).

Merci de vos réponses .

[Kolis]

Bonsoir !
Comme ta question concerne la fonction je dirais que la fonction réciproque est

[Tayyyy]

f(x) = -5x+9/x plutôt erreur de frappe, désolé ^^'

[Ben314]

Salut,
Lorsque l'on demande de montrer qu'une certaine fonction f:A->B est bijective et de déterminer sa bijection réciproque, ben y'a pas trop le choix concernant la méthode (par contre, si on demande uniquement de montrer que f est bijective, là, il peut y avoir plusieurs façons d'aborder le problème).

Et "la" méthode, ben c'est évidement... la définition de ce qu'est une bijection : On prend un y quelconque de l'ensemble d'arrivé et il faut montrer que ce y admet un unique antécédent dans l'ensemble de départ.
Ici, on prend donc un y dans [−124,64 ; −23,2] et il faut montrer qu'il existe un unique x appartenant à [5;25] tel que f(x)=y et c'est cet unique x qui est l'image de y par la bijection réciproque f^(-1)

Et rien qu'en sachant ça, ça permet de voir que ton résultat f^(-1)(y)=9/(y+5) est clairement faux vu que si je prend un y au pif dans [−124,64;−23,2] , par exemple -100, il est évident que 9/(-100+5) n'est pas dans l'intervalle [5;25].

Montre nous un peu comme tu as fait pour résoudre où est fixé (i.e. c'est un paramètre et pas une inconnue) et où on cherche les éventuelles solution qui soient dans l'intervalle [5;25].

[Tayyyy]

j'ai fait tout simplement :

f(x) = y
-5x+9/x = y
9 = yx + 5x
9 = x(y+5)
x = 9/(y+5)

Mais du-coup vu que c'est pas ça je ne connais pas la démarche a adapter...

[Ben314]

Bon, ben... il faut retourner au collège...
Partant de , si tu ajoute 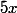des deux cotés ça donne , puis, si tu multiplie les deux membres de l'égalité par , ça donne et le terme de gauche, si tu le développe, il donne et pas .

[Tayyyy]

Oui excusez mon inattention ...
Donc on a :
xy+5x²=9

Mais je ne vois pas du tout comment arrivé à :

f^(-1)(x) = (x-sqrt(x^2+180))/(-10).

[Ben314]

Tu es sensé en faire quoi de l'équation xy+5x²=9 ? (La réponse est dans un des posts çi dessus)

Et de façon générale, le maths, c'est non seulement (un peu) faire des calculs, mais aussi (surtout) de ne jamais perdre de vu le pourquoi on fait ces calculs là et à quoi on voudrait qu'ils conduisent.

[Tayyyy]

Faut trouver f(x)=y avec y appartenant à [-124.64 , 223.2)
donc que f^(-1)=x avec x appartenant à [5,25]
On peut voir un polynôme, je pense pas que ce soit ça, désolé je ne vois pas ...

[Ben314]

Faut trouver f(x)=y avec y appartenant à [-124.64 , 223.2)
donc que f^(-1)=x avec x appartenant à [5,25]
On peut voir un polynôme, je pense pas que ce soit ça, désolé je ne vois pas ...

Si c'est ça que tu as à l'esprit concernant l'objectif des calculs que l'on mêne, alors effectivement, c'est très très très mal barré :
Déjà, autant trouver la valeur d'un réel ou l'expression d'une fonction, ou la dérivée d'une expression, ben ça je comprend ce que ça signifie, autant "trouver une égalité", ben je vois pas ce que ça peut vouloir dire.
Ensuite le "... que f^(-1)=x...", c'est complètement incohérent vu que f^(-1) c'est une fonction et que x c'est un réel : c'est exactement comme si tu disait que ton poids c'est 3h25...

Donc, bis et répéta : pour montrer que f:A->B est bijective (ou pas) et déterminer son éventuelle bijection réciproque, on applique la définition :
On prend un élément y de B (quelconque, mais fixé : c'est un paramètre et pas une variable) et on cherche son(ou ses) antécédent(s), c'est à dire que l'on résous l'équation f(x)=y (où, bien sûr, on cherche le(s) x dans A). Si quelque soit le y de B, il y a une unique solution à cette équation, alors f est bijective et le x solution de l'équation est l'image de y par f^(-1) : f^(-1)(y)=x.

[Tayyyy]

-5x²+yx-9=0
Delta=y²-180

Donc avec la forme : (-b(-+)sqrt(delta)/2a
on trouve :
(-y(+-)sqrt(y²-180))/-10 c.q.f.d
et donc on choisis entre + ou - par rapport aux intervalles données, c'est bon j'ai trouvé merci !