Bonsoir,
Je dois trouver le reste de la division euclidienne de 200^539 par 17.
Suivant la méthode donnée par le professeur, j'ai fait :
* 1ère étape : Division euclidienne de 200 par 17.
200=11x17+13
200 congru à 13 modulo 17
* 2ème étape : Division euclidienne de 13^n (n entier naturel positif) par 17 pour trouver un reste de 1
13^2 congru à 16 modulo 17
13^3 congru à 4 modulo 17
13^4 congru à 1 modulo 17
* 3ème étape : Division euclidienne de l'exposant, 539, par 4 (exposant trouvé lors de l'étape précédente)
539 = 4x134+3
On aboutit donc à 200^539 congru à 13^539
congru à (13^4)^134x13^3
congru à 1+ ?????????????????
Ma question est la suivante : Si je laisse 13^3 en le calculant, j'obtient 1x 2197, ce qui est bien naturellement impossible. Je serais tentée d'utiliser le reste trouvé à l'étape 2 (13^3 congru à 4 modulo 17) pour que mon reste soit cohérent mais je ne sais pas si j'ai le droit et encore moins si c'est la bonne méthode...
Qu'en pensez-vous ?
lesmathsenfolie
Division euclidienne (spé maths)
10 messages
- Page 1 sur 1
 Division euclidienne (spé maths)
Division euclidienne (spé maths)
Modifié en dernier par lesmathsenfolie le 29 Sep 2016, 21:54, modifié 2 fois.
“Les mathématiques ne sont pas une moindre immensité que la mer.” VICTOR HUGO
Re: Division euclidienne (spé maths)
Bonjour,
comment se fait-il que tu aies 539 dans ton énoncé de départ et qu'ensuite tu fasses tes calculs avec 559 ?
comment se fait-il que tu aies 539 dans ton énoncé de départ et qu'ensuite tu fasses tes calculs avec 559 ?
Re: Division euclidienne (spé maths)
et aussi peut-être revoir les règles de calcul sur les exposants ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Division euclidienne (spé maths)
annick a écrit:Bonjour,
comment se fait-il que tu aies 539 dans ton énoncé de départ et qu'ensuite tu fasses tes calculs avec 559 ?
Oui effectivement, erreur de saisie de ma part, c'était bien 539 mais les calculs sont exacts!
“Les mathématiques ne sont pas une moindre immensité que la mer.” VICTOR HUGO
Re: Division euclidienne (spé maths)
zygomatique a écrit:et aussi peut-être revoir les règles de calcul sur les exposants ...
Comment ça?
“Les mathématiques ne sont pas une moindre immensité que la mer.” VICTOR HUGO
Re: Division euclidienne (spé maths)
Oui, je m'en souviens,j'obtiens donc 13^539=13^(4x134+3)=(13^4)^ 134 x 13^3
Sachant que 13^4 est congru à 1, j'obtiens donc 1^134 x 13^3 = 1x13^3.
Je cherche à me "débarasser" du 13^3, sachant qu'il est congru à 4 modulo 17 et ma question est de savoir si je peux écrire que c'est congru à 4 modulo 17 pour le reste final ?
Sachant que 13^4 est congru à 1, j'obtiens donc 1^134 x 13^3 = 1x13^3.
Je cherche à me "débarasser" du 13^3, sachant qu'il est congru à 4 modulo 17 et ma question est de savoir si je peux écrire que c'est congru à 4 modulo 17 pour le reste final ?
“Les mathématiques ne sont pas une moindre immensité que la mer.” VICTOR HUGO
Re: Division euclidienne (spé maths)
Bonjour,
Oui, bien sûr. C'est le but. Et 4 est bien le reste de la division euclidienne de ... par ... , car 4 est compris entre quoi et quoi ?
Oui, bien sûr. C'est le but. Et 4 est bien le reste de la division euclidienne de ... par ... , car 4 est compris entre quoi et quoi ?
Re: Division euclidienne (spé maths)
il est compris entre 0 et 17... merci beaucoup, mon problème est résolu !!
“Les mathématiques ne sont pas une moindre immensité que la mer.” VICTOR HUGO
Re: Division euclidienne (spé maths)
Félicitations 
En relisant votre exercice, je me rends compte que vous étiez très guidé (c'était carré).
Etes vous capable à présent de déterminer sans guide le reste de divisé par
divisé par 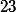

En relisant votre exercice, je me rends compte que vous étiez très guidé (c'était carré).
Etes vous capable à présent de déterminer sans guide le reste de

10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
