Sur l'idée, c'est déjà nettement mieux, mais la rédaction laisse franchement à désirer et je pense que c'est ça qui fait que tu es bloqué :
Simpi a écrit:1) le fait que
 \text{ait n racines})
implique que les

verifie
 = 0)
ça, c'est absolument pas clair du tout ce que ça signifie vu qu'en particulier tu n'as pas quantifié les variables

et

qui apparaissent dans cette phrase.
- Le

, on peut considérer qu'il est sous entendu que c'est une matrice
appartenant à l'ensemble U, mais à mon avis, ça serait bien mieux de l'écrire en toute lettre, ne serait-ce que du fait que plus tard, une fois plongé dans d'éventuels calculs techniques, tu risque d'oublier que A est dans U.
- Ce n'est pas "
)
qui a n racines (distinctes)" mais "La fonction polynomiale \lambda\mapsto F(\lambda,A) qui a n racines distinctes". De nouveau, on peut trouver que c'est de l'enc... de mouche de faire la différence entre les deux, mais je pense que c'est important pour raisonner correctement. Pour que
)
ait un sens, il faut connaitre F (là, c'est O.K), connaitre A (c'est O.K. aussi : c'est une matrice fixée de U) et connaitre

et là, c'est pas O.K. du tout vu où on en est du laïus.
- Et là où on voit encore plus que ça déconne, c'est sur la fin de ta ligne, quand tu écrit "... vérifie
=0)
", c'est pour quel(s) lambda que cette égalité est vérifiée ? Surement pas "pour tout lambda réel" (ce qui est en général sous entendu quand on ne précise pas à quel ensemble appartient une variable), et si c'est "pour tout

valeur propre de la matrice A" alors tu n'as fait que réécrire la définition de ce qu'est une valeur propre et tu n'as absolument pas traduit quoi que ce soit de lié au fait que "A admet n valeurs propres distinctes".
Bref, ce qu'il faut écrire, c'est :
Correct a écrit:1) Si

est dans

alors le fait que la fonction polynomiale
)
ait n racine distinctes implique qu'il existe n réels distincts

tels que
 = F(\lambda_2, A) =...=F(\lambda_n, A) =0)
Ensuite, ton 2), c'est bien (à peu prés) ça qu'il faut écrire, mais il faut l'écrire avec les différents

et pas comme tu l'écrit avec un

"quelconque".
Arrivé à ce point, ce qu'il se dégage, c'est que le 3), on ne va pas l'appliquer UNE fois, mais n fois : une fois pour chaque

ce qui va nous donner n voisinages
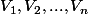
de A ainsi que n fonctions

.
Et il reste un (petit) truc à démontrer pour que ce soit fini...
