(Il)logique?

[Arno21]

Bonjour,

pourquoi l'assertion suivante est fausse :

x y
x+y>0




alors que celle ci est vraie.

x y
x+y>0

J'ai dû rater un épisode... en quoi l'ordre des et change le sens de l'assertion (car il semble bien que c'est de ça dont il s'agit).
Merci par avance d'éclairer ma lanterne.

[beagle]

ben dans la première le il existe x définit le x en premier,
et ensuite celadevrait ètre valable pour tous les y,
alors forcément non,
si je dis il existe 3 ou il existe -7 ou il existe un autre truc,
ben jamais tous les y de IR feront 3+y positif ou -7+y positif ou truc définit + y positif

[mashke]

Pour la première,
prends y=-x donc on ne peut pas prendre n'importe quel y.
Pour la deuxième,
prends y=-x+1 donc il existe bien un y tel qu'on ait l'inégalité.

[Lostounet]

Bonjour,

pourquoi l'assertion suivante est fausse :

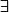
x y
x+y>0
alors que celle ci est vraie.

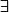
x y
x+y>0

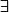
J'ai dû rater un épisode... en quoi l'ordre des et change le sens de l'assertion (car il semble bien que c'est de ça dont il s'agit).
Merci par avance d'éclairer ma lanterne.

Salut. L'ordre des quantificateurs 'il existe' et 'pour tout' change le sens de la proposition. Nous allons expliquer pourquoi sur ton exemple.

La première te dit qu'il existe un nombre x réel fixe absolu tel que pour tout y, x+y>0
Donc en gros, elle dit que tu peux trouver un nombre x pour lequel tous les y réels seront tels que x+y>0
Donc y>-x

C'est faux car si y est plus petit que -x (on peut toujours prendre y plus petit que le nombre -x fixe car y appartient à R) tu auras y<-x et y+x<0

Si tu me dis je prends x=5 alors pour tout y de R on a x+y>0 donc 5+y>0 et y>-5 il suffit de voir que pour y=-7 la propriété n'est pas vérifiée.
Tu changeras de x, je prendrais toujours un y plus petit que -x pour contrer ta proposition. Elle est fausse.

Pour la deuxième c'est différent. Elle te dit que quel que soit le nombre choisi x, il existera un nombre y qui dépend de x tel que x+y soit positif.
C'est logique et même intuitif

Donne moi un nombre genre x=-390
Ben il existe y=391 tel que x+y=1>0

[Arno21]

Merci à vous 3, et tout particulièrement Lostounet.
C'est limpide dans ma tête ; je "lisais" mal les assertions, un peu comme si ces quantificateurs se comportait comme des éléments de phrases:

"Ce soir, j'ai mangé des pommes."
"J'ai mangé des pommes, ce soir."

Voilà comment je voyais les choses.

Encore merci.

[Ben314]

Salut,
Même en Français, il est bien clair que l'ordre dans lequel on met les quantificateur change le sens de la phrase :

1) Toute les personnes présentes ont lu au moins un article de math
( personne P, article A tel que P a lu A)

2) Il y a au moins un article de math qui a été lu par toutes les personnes présentes
( article A tel que personne P, P a lu A)

Tu fait pas de différence entre les deux phrases ?

Et le problème, c'est que dans "ce soir j'ai mangé des pommes", je vois pas trop où se situe les deux quantificateurs.
A la limite, on peut en voir un (existentiel) dans le "des pommes" (i.e. il existe des pommes que j'ai mangé ce soir) mais comme il n'y en a pas d'autres, je vois pas trop ce qu'on peut permuter...

[Arno21]

C'est très clair comme cela aussi; je ne lisais pas les assertions telles qu'elles devaient être lues.
Merci Ben !

[nodgim]

Perso, j'ignorais totalement cette subtile nuance. Je pensais que l'ordre était indifférent. Comme quoi...

[Ben314]

A mon avis, LE exercice a faire pour bien comprendre que l'ordre des quantificateurs est super important est le suivant :

Soit une partie de .
On considère les 4 propositions suivantes :




1) Déterminer lesquelles de ces propositions sont vraies lorsque , puis lorsque , puis lorsque et enfin lorsque .
2) Donner la liste de toutes les proposition de la forme ou (=négation) ou ou qui sont vraies pour toutes les parties de .

[Arno21]

Merci bien Ben, je m'y attèlerai et posterai mes réponses.