Une petite précision sur cette somme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cond2016
- Membre Naturel
- Messages: 10
- Enregistré le: 26 Aoû 2016, 18:15
-
 par Cond2016 » 17 Sep 2016, 13:55
par Cond2016 » 17 Sep 2016, 13:55
Bonjour,
C'est surement une question simple, mais elle m'a mit le doute...
Pour une discussion de cas, je dois montrer :
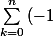^k})
Du coup j'ai fais ça :
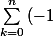^k}=\sum_{0\leq 2k\leq n}^{}{(-1)^{2k}} + \sum_{0\leq 2k+1\leq n}^{}{(-1)^{2k+1}})
Et là du coup je sais pas comment conclure... Je me rend bien compte que ça fait soit 0 soit 1, mais je n'ai aucunes idée de comment le justifier.
Dois-je simplement dire que
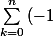^k})
est égal à 0 pour n pair et 1 pour n impair ? Ou devrais-je le justifier autrement ?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 17 Sep 2016, 14:07
par Pseuda » 17 Sep 2016, 14:07
Bonjour,
Tu peux simplement le montrer par récurrence sur n, en distinguant n pair et n impair.
Après initialisation, supposons que pour n pair, la somme est égale à 0, et que pour n impair la somme est égale à ? , alors pour n+1...
-
Cond2016
- Membre Naturel
- Messages: 10
- Enregistré le: 26 Aoû 2016, 18:15
-
 par Cond2016 » 17 Sep 2016, 14:31
par Cond2016 » 17 Sep 2016, 14:31
Comme c'est dans une distinction de cas, et que ce n'est pas du tout le but de l'exercice, je pense que je vais justifier tout simplement par une phrase.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 17 Sep 2016, 14:58
par anthony_unac » 17 Sep 2016, 14:58
Cond2016 a écrit:Dois-je simplement dire que
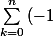^k})
est égal à 0 pour n pair et 1 pour n impair ? Ou devrais-je le justifier autrement ?
Bonjour,
Prenons une valeur de

impaire mettons
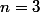
, il vient :
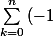^k}=(-1)^0+(-1)^1+(-1)^2+(-1)^3=1-1+1-1=0)
Ce contre exemple suffit à revoir votre conclusion n'est ce pas ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 17 Sep 2016, 15:23
par chan79 » 17 Sep 2016, 15:23
salut
C'est aller chercher des complications et il faut sans doute rédiger autrement, mais tu pourrais démontrer par récurrence que ta somme est égale à
^n }{2})
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 18 Sep 2016, 11:51
par Pseuda » 18 Sep 2016, 11:51
chan79 a écrit:salut
C'est aller chercher des complications et il faut sans doute rédiger autrement, mais tu pourrais démontrer par récurrence que ta somme est égale à
^n }{2})
Bonjour,
En effet. On peut le voir aussi comme la somme des termes d'une suite géométrique, et on obtient... le même résultat.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
