Matrice d'un endomorphisme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
 par Hoog » 08 Oct 2006, 17:02
par Hoog » 08 Oct 2006, 17:02
Soit E le IR-ev des polynômes de degé inférieur ou égal à 2. Soit

l'endomorphisme de E défini par pour tout p de E et pour tout x de IR par :
+bxtp'(x-t)+cx^2t^2 p^{(2)}(x-t)]\, dt)
où a, b et c sont des réels. Soit la base canonique de E
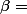
{

} où :
 = 1 ;<br /> p_1(x) = x ; <br /> p_2(x) = x^2) (PS : j'arrive pas à faire p'' en TEX)
(PS : j'arrive pas à faire p'' en TEX)1. Déterminer la matrice A de l'endomorphisme

dans la base

.
2. A quelle(s) condition(s) sur a, b et c l'endomorphisme

est-il bijectif ?
merci pour votre aide :hein: !...
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 08 Oct 2006, 17:17
par Quidam » 08 Oct 2006, 17:17
Hoog a écrit:](x)=\int_{0}^{1} [ap(t)+bxtp'(x-t)+cx^2t^2 p^{(2)}(x-t)]\, dt)
Ben tu prends un élément de E :
=\Large (\alpha p_2+\beta p_1+\gamma p_0)(x)=\alpha x^2+\beta x+\gamma)
, tu évalues P'(x) et P''(x)
et tu développes :
](x)=\int_{0}^{1} [a(\alpha t^2+\beta t+\gamma)+bxtP'(x-t)+cx^2t^2 P^{(2)}(x-t)]\, dt)
Tu vas forcément trouver quelque chose du genre :
)(x) = \alpha ' x^2 + \beta ' x +\gamma')
les trois coefficients dépendant des
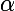
,
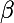
et
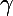
et tu auras la matrice de ton endomorphisme.
Mais les calculs, c'est toi qui dois les faire, pas moi !
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
 par Hoog » 08 Oct 2006, 17:20
par Hoog » 08 Oct 2006, 17:20
:id:
Je me lance ! Merci pour le déblocage !
-
Hoog
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Sep 2006, 00:02
-
 par Hoog » 08 Oct 2006, 18:18
par Hoog » 08 Oct 2006, 18:18
Bon, je trouve (aux erreurs de calcul près) :
](x) = (\alpha b+\frac{2\alpha c}{3})x^2 + (\frac{b\beta}{2}-\frac{2\alpha b}{3})x + (\frac{a\alpha}{3}+\frac{a\beta}{2}+a\gamma) \,)
(avec tes notations)
euh... ça donne quoi comme matrice ? :dingue:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 08 Oct 2006, 18:43
par Quidam » 08 Oct 2006, 18:43
Hoog a écrit:Bon, je trouve (aux erreurs de calcul près) :
](x) = (\alpha b+\frac{2\alpha c}{3})x^2 + (\frac{b\beta}{2}-\frac{2\alpha b}{3})x + (\frac{a\alpha}{3}+\frac{a\beta}{2}+a\gamma) \,)
(avec tes notations)
euh... ça donne quoi comme matrice ? :dingue:
Ben, bien sûr, je ne vérifie pas, je te fais confiance !
Donc :
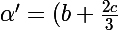 \times \alpha)
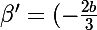\times \alpha + (\frac{b}{2}) \times \beta)
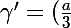\times \alpha + (\frac{a}{2})\times \beta + (a) \gamma)
ben tu l'as ta matrice, non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités