Démontrer par récurrence

[Firoda]

Hello world voilà jai un exo noté pour mardi , si quelqu'un pouvais me venir en aide. Il s'agit de démontrer par récurrence que pour tout entier naturel n, un>ou= à 1 et on a comme information f(x) = 4x-2/x+1 et Un +1 = 4Un-2/Un+1 voilà pour ceux ou celles qui peuvent m'aider j'ai déjà commencer les trois étapes soit initialisation que je pense à voir réussi mais je bloque à l'hérédité qqun pourrait t'il m'expliquer

[siger]

Bonjour

1- utilise les parentheses!!!!!
f(x) = 4x-2/x+1 veut dire
4x -2/(x+1) ou 4x -(2/x ) + 1 ?
de meme Un+1 =U(n+1) ou Un + 1 ?

2-dis nous donc ce que tu as fait

[capitaine nuggets]

Salut !

Pour l'hérédité, supposes que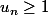 et montre, en utilisant l'expression de en fonction de , que .

[Firoda]

Ah excusez moi et bah c'est (4Un+1)/ (Un+1) et alors j'ai d'abord U0=3 donc U0>1 alors P0 est vraie il me semble ensuite jai supposée que Pk était vraie donc que Uk>ou= à 1 donc il faut montrer que (Uk+1) >ou = à 1 et j'imagine que f(Uk) >ou = à 1 voilà pour l'instant mon raisonnement ensuite j'ai essayé de remplacer les x de ma fonction par K et j'ai finis par obtenir 4 - 6/K+1 > 1 donc je suis pas du tout sur de ce que je fais la après j'ai fais delta et je me retrouve avec x1 = 1,309 et x2=0,19 et voila mais jai surement du me tromper