Aide sur quelques limites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cybergzu
- Messages: 4
- Enregistré le: 08 Sep 2016, 15:50
-
 par cybergzu » 08 Sep 2016, 15:56
par cybergzu » 08 Sep 2016, 15:56
Bonjour à tous,
J'aurai besoin d'une petite (grande) aide afin de résoudre quelques limites. Je sait qu'elles sont simples mais on va dire que mon niveau est assez simple alors soyez indulgents par pitié

1. lim (x->+inf) (7x−1)/(racine cubique(5x^3+4x−2)),
2. lim (x->0)(1−sinx)^(1/x),
3. lim (x->+inf) (1+(2x+5)/(2x−6)+(x+1)/(-x−1))^((x^2−2)/(x+1))
Merci!

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 08 Sep 2016, 16:13
par anthony_unac » 08 Sep 2016, 16:13
Bonjour,
1. Et si vous tentiez de factoriser par

le radicande

-
cybergzu
- Messages: 4
- Enregistré le: 08 Sep 2016, 15:50
-
 par cybergzu » 08 Sep 2016, 16:22
par cybergzu » 08 Sep 2016, 16:22
ce qui donnerai:
(7x−1)/(x * racine (5+4/x^2−2/x^3))
Mais je dois me débarrasser de la racine non?

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 08 Sep 2016, 16:24
par anthony_unac » 08 Sep 2016, 16:24
Pourquoi s'en débarasser, elle ne nous gêne plus, non ?

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 08 Sep 2016, 16:31
par anthony_unac » 08 Sep 2016, 16:31
Ce qui vous gêne à la base c'est une forme indéterminée du type
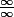
Mais à présent ...

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 08 Sep 2016, 16:39
par anthony_unac » 08 Sep 2016, 16:39
2. Et si on transformait le nombre 1 (dans l'expression : 1-sin(x)) en une addition (de deux termes) contenant du cosinus et du sinus ?
Cela ne vous rappelle pas une identité remarquable ?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Sep 2016, 17:01
par zygomatique » 08 Sep 2016, 17:01
anthony_unac a écrit:Bonjour,
1. Et si vous tentiez de factoriser par

le radicande

cybergzu a écrit:ce qui donnerai:
(7x−1)/(x * racine (5+4/x^2−2/x^3))
Mais je dois me débarrasser de la racine non?
on se fout de la racine (qui ne pose aucun problème)
mais ce qu'on fait au dénominateur (mettre x en facteur) pourquoi ne pas le faire au numérateur
donc : et si on factorisait par x au numérateur ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
cybergzu
- Messages: 4
- Enregistré le: 08 Sep 2016, 15:50
-
 par cybergzu » 08 Sep 2016, 17:19
par cybergzu » 08 Sep 2016, 17:19
Si je factorise par x au numerateur j'obtiens une limite de type k/0 non? du coup ce serait faire une étude de signe pour la résoudre.
pour la seconde, en remplaçant 1 par cos^2+ sin^2, j'obtiens donc cos^2(x)+ sinx(sinx-1), la limite serait 1?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Sep 2016, 17:44
par zygomatique » 08 Sep 2016, 17:44
mais un peu de sérieux !!
1/ tu calcules la limite où ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
cybergzu
- Messages: 4
- Enregistré le: 08 Sep 2016, 15:50
-
 par cybergzu » 08 Sep 2016, 17:55
par cybergzu » 08 Sep 2016, 17:55
Désolé mais c'est la fin de la journée et je suis creuvé, bref.
Si x tend vers plus l'infini, le numérateur tend vers 7 et le denominateur vers racine(5). Donc pour la limite ok.
Mais pour la seconde?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 08 Sep 2016, 18:05
par zygomatique » 08 Sep 2016, 18:05
prendre le logarithme puis travailler avec des équivalents :
au voisinage de 0 ::

 \approx ...)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 09 Sep 2016, 11:32
par aymanemaysae » 09 Sep 2016, 11:32
Bonjour,
Pour le deuxième exercice je propose cette solution qui n'utilise que les notions abordées en terminale.
Dans un voisinage épointé de

(
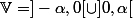
) avec

, on a :
)^{\frac{1}{x}} = \exp(\ln((1-\sin(x))^{\frac{1}{x}})) = \exp(\frac{1}{x}\ln(1-\sin(x))))
,
on a aussi
) = \lim_{x\rightarrow 0}\dfrac{\ln(1-\sin(x))}{x} = \lim_{x\rightarrow 0}\dfrac{\ln(1-\sin(x)) - 0}{x - 0} = - \frac{\cos(0)}{1-\sin(0)} = - 1)
car
) - 0}{x - 0})
est la dérivée de
))
au point
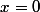
.
donc
)^{\frac{1}{x}} = \lim_{x\rightarrow 0} \exp(\frac{1}{x}\ln(1-\sin(x))) = \exp(-1))
.
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 09 Sep 2016, 11:51
par aymanemaysae » 09 Sep 2016, 11:51
Bonjour;
pour le premier exercice, on a :
}{\sqrt[3]5 x \sqrt[3]{1+ \frac{4}{5x^2}-\frac{2}{5x^3}}} = \lim_{x\rightarrow + \infty} \dfrac{7x}{\sqrt[3] 5 x} \dfrac{1-\frac{1}{7x}}{ \sqrt[3]{1+ \frac{4}{5x^2}-\frac{2}{5x^3}}})
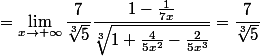
car
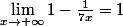
et
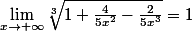
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
