limte a l'infini de
Limite
23 messages
- Page 1 sur 2 - 1, 2
limite
par Bouhachmoud » 03 Sep 2016, 18:28
Bonjour, j'arrive a résoudre cet limite c qlq'un peut sauver la situation
limte a l'infini de})
limte a l'infini de
Re: limite
par zygomatique » 04 Sep 2016, 01:41
salut
déjà si |x| >= 1 alors ....
ensuite on peut prendre le logarithme et faire un dl (ou un équivalent)
déjà si |x| >= 1 alors ....
ensuite on peut prendre le logarithme et faire un dl (ou un équivalent)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: limite
par zygomatique » 04 Sep 2016, 14:55
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: limite
par Bouhachmoud » 05 Sep 2016, 10:05
y a pa d’énoncé c un question seul dans un concours(QCM) avev 4 choix :
1--f est continue en tout points Xn=2*n^2
2--f est discontinue en tout points Xn=2*n^2
3--f est dérivable en tout points Xn=2*n^
4--f est dérivable sur R*
1--f est continue en tout points Xn=2*n^2
2--f est discontinue en tout points Xn=2*n^2
3--f est dérivable en tout points Xn=2*n^
4--f est dérivable sur R*
Re: limite
par Razes » 05 Sep 2016, 10:47
Mais ceci n'a rien à voir avec le premier énoncé. On ne te demande pas de calculer une limite. J'imagine que:
=\prod_{0}^{n}{(1+x^2^k)})
Tu es en supérieur et tu ne te rends pas compte de ce que tu fais en transformant l'énoncé.
Tu es en supérieur et tu ne te rends pas compte de ce que tu fais en transformant l'énoncé.
Modifié en dernier par Razes le 05 Sep 2016, 14:51, modifié 1 fois.
Re: limite
par Bouhachmoud » 05 Sep 2016, 13:55
Ohh je m'excuse j'ai pa fait attention
aussi pour cette limite y a pa d'énoné , ils ont me demandé la résultat final L = ??
aussi pour cette limite y a pa d'énoné , ils ont me demandé la résultat final L = ??
Re: limite
par Razes » 05 Sep 2016, 15:25
Posons: =x^2^n)
Nous avons:=\prod_{0}^{n}{(1+u_n(x))})
, cherchons dans quelles conditions notre expression converge et quelle serait sa limite.
Supposons que)
converge vers )
, nous avons la relation =(1+u_n(x))P_n(x))
, en passant à la limite, nous aurons donc:
=(1+\lim_{n\to \infty} u_n(x))P(x)\Leftrightarrow P(x)\lim_{n\to \infty} u_n(x)=0)
Les cas possibles sont:
=0)
Ce qui veut dire que la suite)
est nulle à un certain rang ou que =-1)
, ce qui est impossible car est positive ( =x^2^n=(x^n)^2)
)
\neq0)
Donc :=0)
ce qui entraine que 
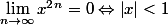
J'espère que ceci te mettra sur la voie
Nous avons:
Supposons que
Les cas possibles sont:
Ce qui veut dire que la suite
Donc :
J'espère que ceci te mettra sur la voie
Re: limite
par Razes » 06 Sep 2016, 08:33
Matt_01 a écrit:T'es sur que c'est pas?
Que dit l'énoncé?
Bouhachmoud a écrit:Bonjour, j'arrive a résoudre cet limite c qlq'un peut sauver la situation
limte a l'infini de
C'est l'écriture
Re: limite
par Razes » 07 Sep 2016, 00:25
Bonsoir Bouhachmoud,
}=(1+1)(1+x^2)(1+x^4)\cdots (1+x^{2n})=2(1+x^2)(1+x^4)\cdots (1+x^{2n}))
, multiplions l'expression par )
Nous obtenons:
\prod_{0}^{n}{(1+x^2^k)}&=& 2(1-x^2)&(1+x^2) &(1+x^4) &\cdots & (1+x^{2n}) \\ &=&& 2(1-x^4) &(1+x^4) &\cdots&(1+x^{2n}) & \\ &=&& &2(1-x^8) &\cdots&(1+x^{2n}) & \\ &=& & & &\cdots & \cdots\\ &=& & & & &2(1-x^{4n}) \end{matrix})
Donc:
}=\dfrac{2(1-x^{4n})}{(1-x^2)})
La condition de convergence reste la même
D'où:}=\dfrac{2}{(1-x^2)})
Nous obtenons:
Donc:
La condition de convergence reste la même
D'où:
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :