Probabilité

[huyhuyge]

Bonjour à tous !

J'aimerais savoir quelle est la probabilité d'obtenir avec un dé non pipé uniquement deux six en k lancers dont 1 au k-ième lancers .

Pour moi on se rapproche de quelque chose comme : ( 5/6)^(k-2) * 1/6 ( pour le 6 quelconque) * X ( et la je bloque)

Merci à vous pour un éventuel coup de pouce !

[zygomatique]

salut

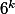
au total il y a issues

il y a issues contenant deux six

parmi celles-ci il y en a k - 1 contenant un six à la k - 1-ième place et l'autre à la dernière place

donc


ce me semble-t-il ....

[beagle]

loi binomiale c'est la proba de base d'un évènement :
p^k * q^(n-k)
et ensuite on multiplie cette proba de base par le nombre d'occurrence de cet évènement donc par le C(k,n)

alors ici 2 fois le six c'est (1/6)² et pas de six pendant (k-2) c'est (5/6)^(k-2)
ça c'est l'évènement de base d'avoir deux six seulement sur les k
combien d'occurrence maintenant de ce truc
ben 1 emplacemnt est fixe , le k-1, j'ai pas le choix, il me reste liberté de choisir le deuxième emplacement du 6 dans les (k-1) emplacements restants
au total c'est=
(k-1) x (1/6)² x (5/6)^(k-2)

[beagle]

J'ai fait 1/6 au k-1 ièm j'ai mal lu
bon c'est pareil en plus simple:
de 1 à k-1 binomial classique où je veux avoir 1 seul 6
et dernier lancer faut du 6 donc fois 1/6

première partie:
Choisir 1 emplacement dans (k-1) fois 1/6 fois 5/6 puissance k-1-1
puis dernier lancer 1/6

[chan79]

salut
la même chose dit autrement
nombre de cas possibles
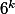
nombre de cas favorables:
pour le dernier, pas le choix
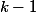
positions pour l'autre 6
Pour les (k-2) autres, on a 1, 2, 3, 4, ou 5
donc

donc la proba cherchée est

[zygomatique]

oui j'ai mal conclus ...