Étape d'un calcul

[lrnt00]

Bonjour, je suis bloqué à cette étape:
(Rac(n+1)-Rac(n))(Rac(n+1)-rac(n))
Dans la correction, la réponse est 1, je ne comprend aps comment on passe de ça à 1, si vous voulez bien m'aider

[Gisé]

Salut,

Tu n'as pas dû voir que c'était la même quantité en haut et en bas

[beagle]

ou alors tu n'as pas vu que d'un coté on avait un + et de l'autre un -

comme dans l'identité remarquable:
(a+b) (a-b) = a² - b²

[Gisé]

Oups désolé, j'ai cru à une fraction ...

Dans ton premier post, c'est la même quantité dans le membre de droite que dans celui de gauche.

Il faut considérer , puis suivre l'indication de beagle.

[zygomatique]

pourquoi faire du multi-post ?

[lrnt00]

Je ne comprend pas vos réponses, enfaite si ça peut aider c'est une fraction:
((Rac(n+1)-Rac(n))(Rac(n+1)-rac(n)))/Rac(n+1)+Rac(n)
Le résultat étant: 1/Rac(n+1)+Rac(n)

[lrnt00]

pourquoi faire du multi-post ?

Comment ça? C'est à dire que je pose bcp de questions?

[Gisé]

Je ne comprend pas vos réponses, enfaite si ça peut aider c'est une fraction:
((Rac(n+1)-Rac(n))(Rac(n+1)-rac(n)))/Rac(n+1)+Rac(n)
Le résultat étant: 1/Rac(n+1)+Rac(n)

Je ne comprends pas ta question.

Tout t'a été expliqué !

Il y a une erreur au numérateur. C'est l'expression que j'ai donnée dans mon précédent message qu'il faut considérer.

Ton expression est :



MULTI-POST = tu postes le MÊME SUJET sur deux fils différents. Tu trompes ainsi ceux qui te répondent.

[lrnt00]

Dans la correction de l'exercice ce n'était pas comme ça au numérateur, Il y avait ce que je vous ai Indiquer

[Gisé]

Donne-nous l'énoncé exact, ça sera tellement plus simple !!!

[lrnt00]

Mais ça sera beaucoup plus long! Mais bon.
"Montrez que Un EST croissante, avec Un= ( n*Rac(n)-1000)/n avec n>ou= à 1."

[Gisé]

Et donc, quel est ton raisonnement ... Ça n'avance pas hein !

Sinon, pour revenir à la question de base, il suffit de montrer que :



On te l'a dit, applique simplement l'identité

[lrnt00]

Bon je me suis pas fais comprendre alors.
Pour répondre à la consigne il faut faire Un+1-Un, c'est ce que j'ai fais sauf que j'ai bloqué à une étape j'ai regardé la correction, & il y avait écrit ce que je vous ai indiqué! Alors je comprend pas pourquoi vous me ressortez (a+b)(a-b), puisque dans la correction on a plutôt: ((a-b)(a-b))/a+b
http://www.academie-en-ligne.fr/Ressour ... rcices.pdf C'est A la page 12, question b c'est la correction

[zygomatique]

salut

Pour répondre à la consigne il faut faire Un+1-Un

1/ que veut dire faire ?
2/ non il suffit ...

mais on peut s'en passer :::



or les fonctions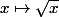 et sont (strictement) croissantes (l'opposé d'une fonction décroissante est croissante)

il en est de même de leur somme ...

[Gisé]

Bon je me suis pas fais comprendre alors.
Pour répondre à la consigne il faut faire Un+1-Un, c'est ce que j'ai fais sauf que j'ai bloqué à une étape j'ai regardé la correction, & il y avait écrit ce que je vous ai indiqué! Alors je comprend pas pourquoi vous me ressortez (a+b)(a-b), puisque dans la correction on a plutôt: ((a-b)(a-b))/a+b
http://www.academie-en-ligne.fr/Ressour ... rcices.pdf C'est A la page 12, question b c'est la correction

Tout simplement parce qu'il y a une erreur dans la correction du CNED pardi !!

Au numérateur, c'est un + et NON un - ...

[lrnt00]

Ah bah voilà! C'est donc pour ça! Bon bah c'est bon alors c'est compris, en tout cas merci pour vos réponses!

[zygomatique]

et je l'avais écrit dans l'autre fil : lycee/etape-calcul-t176041.html

[Lostounet]

pourquoi faire du multi-post ?

Comment ça? C'est à dire que je pose bcp de questions?

Cela signifie qu'il ne faut pas créer deux discussions identiques pour une même question. Car on s'y perd...