Matrice carre
15 messages
- Page 1 sur 1
Re: matrice carre
Bonjour,
si on pose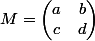 on a
on a 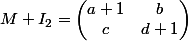 ,
,
donc = \begin{pmatrix} a^2+a+bc&b(a+d+1)\\c(a+d+1)&d^2+d+bc \end{pmatrix}) ,
,
donc il suffit que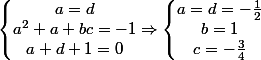 ,
,
donc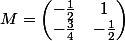 .
.
C'est un exemple parmi d'autres.
si on pose
donc
donc il suffit que
donc
C'est un exemple parmi d'autres.
Re: matrice carre
Bonjour,
Autre façon pour trouver un exemple (en tout cas si les matrices peuvent être complexes, ce qui est a priori vrai vu comment l'énoncé est posé), considérer une matrice 2x2 dont le polynôme caractéristique est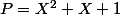 (la matrice diag(a,b) où a et b sont les racines de P convient, par exemple).
(la matrice diag(a,b) où a et b sont les racines de P convient, par exemple).
Autre façon pour trouver un exemple (en tout cas si les matrices peuvent être complexes, ce qui est a priori vrai vu comment l'énoncé est posé), considérer une matrice 2x2 dont le polynôme caractéristique est
Re: matrice carre
salut
je ne sais pas si ça simplifie ...
si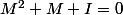 alors M n'est pas l'identité et en multipliant par M - I alors
alors M n'est pas l'identité et en multipliant par M - I alors 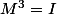
...
je ne sais pas si ça simplifie ...
si
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: matrice carre
Bonjour,
On avait posé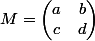 donc
donc \\c(a+d+1)&d^2+d+bc+1 \end{pmatrix}) ,
,
donc = 0\\c(a+d+1) = 0 \end {matrix}) ,
,
Pour que) il faut avoir
il faut avoir  sinon
sinon  et
et  seront des nombres complexes,
seront des nombres complexes,
donc on a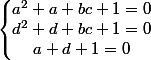 ,
,
 et
et  sont les solutions de l'équation dans
sont les solutions de l'équation dans 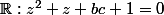 .
.
Si est le discriminant de l'équation, on doit avoir
est le discriminant de l'équation, on doit avoir 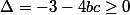 donc on doit avoir
donc on doit avoir  .
.
Donc pour on a
on a 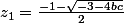 et
et 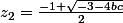 ,
,
donc\in \left\{(\frac{-1-\sqrt{-3-4bc}}{2} , \frac{-1+\sqrt{-3-4bc}}{2}) , (\frac{-1+\sqrt{-3-4bc}}{2} , \frac{-1-\sqrt{-3-4bc}}{2}) : bc \le - \frac{3}{4}\right\})
donc on a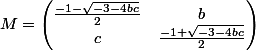 ou
ou 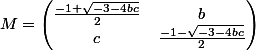 avec
avec  .
.
On avait posé
donc
Pour que
donc on a
Si
Donc pour
donc
donc on a
Modifié en dernier par aymanemaysae le 25 Aoû 2016, 19:38, modifié 3 fois.
Re: matrice carre
Bonjour,
Cette équation n'admet pas de solutions dans (son discriminant vaut -3)
(son discriminant vaut -3) 
aymanemaysae a écrit:
donc on a,
et
sont les solutions de l'équation dans
.
Cette équation n'admet pas de solutions dans
Re: matrice carre
Bonjour,
Vous avez raison : faute d'inattention , c'est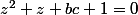 (j'ai rectifié l'erreur) .
(j'ai rectifié l'erreur) .
Merci.
Vous avez raison : faute d'inattention , c'est
Merci.
Re: matrice carre
youssefbls a écrit:exemple de matrice de 2x2 qui verifie : M^2+M+1=0
salut
(M+I/2)²+3/4*I=0
On pose N=M+I/2
cela donne les 4 égalités:
a²+bc=-3/4
b(a+d)=0
c(a+d)=0
a²=d²
exemple1
avec a=0, d=0, b=1 et c=-3/4
N=
soit
M=
exemple2
avec a=-1/2, b=1, c=-1 et d=1/2
N=
soit
M=
exemple3
N=
soit
M=
exemple4
N=
soit
M=
exemple5
M=
Si on se donne un couple (b,c) on peut expliciter les solutions.
Modifié en dernier par chan79 le 25 Aoû 2016, 08:13, modifié 2 fois.
Re: matrice carre
Bonjour !
Un autre point de vue !
Par théorème de Caylay-Hamilton, pour une matrice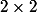 on a
on a 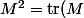M-\mathrm{det}(M)I_2) .
.
La relation proposée est donc équivalente à)M+(1-\mathrm{det}(M))I_2=0) ce qui implique :
ce qui implique :
ou bien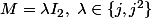 (racines cubiques non réelles de 1)
(racines cubiques non réelles de 1)
ou bien=-1,\;\det(M)=1)
Un autre point de vue !
Par théorème de Caylay-Hamilton, pour une matrice
La relation proposée est donc équivalente à
ou bien
ou bien
Re: matrice carre
Kolis a écrit:Bonjour !
Un autre point de vue !
Par théorème de Caylay-Hamilton, pour une matriceon a
.
La relation proposée est donc équivalente àce qui implique :
ou bien(racines cubiques non réelles de 1)
ou bien
salut
je complète
Parmi les solutions, 4 sont diagonales:
Les deux premières sont bien données par Kolis (premier cas)
Les deux autres ont bien une trace égale à -1 et un déterminant égal à 1
Re: matrice carre
Bonjour,
Si on a) , et comme on avait posé
, et comme on avait posé 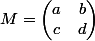
on avait obtenu\\c(a+d+1)&d^2+d+bc+1 \end{pmatrix}) ,
,
donc = 0\\c(a+d+1) = 0 \end {matrix} \Rightarrow \left \{ \begin {matrix} a=z_1 \vee a = z_2 \\d=z_1 \vee d=z_2\\b=0 \vee a+d=-1\\c=0 \vee a+d=-1 \end {matrix}) avec
avec 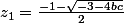 et
et 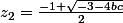 .
.
Si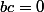 posons
posons 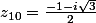 et
et 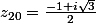 ,
,
on a selon les cas suivants :
selon les cas suivants :
 b=c=0) et
et 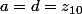
 b=c=0) et
et 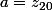 et
et 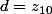
 b=c=0) et
et 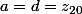
 b=c=0) et
et 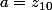 et
et 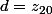
 b=0) et
et 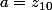 et
et 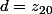 et
et 
 b=0) et
et 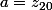 et
et 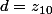 et
et 
 c=0) et
et 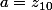 et
et 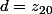 et
et 
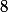 c=0) et
et 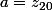 et
et 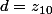 et
et 
 a=z_1) et
et 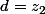 et
et \in \mathbb C^{*2})
 a=z_2) et
et 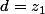 et
et  \in \mathbb C^{*2})
Je crois que je n'ai rien oublié.
Si on a
on avait obtenu
donc
Si
on a
Je crois que je n'ai rien oublié.
Modifié en dernier par aymanemaysae le 25 Aoû 2016, 19:40, modifié 1 fois.
Re: matrice carre
zygomatique a écrit:salut
je ne sais pas si ça simplifie ...
sialors M n'est pas l'identité et en multipliant par M - I alors
...
Bonsoir,
Puisque
Re: matrice carre
Bonsoir,
Merci M.Pseuda pour votre exemple, il m'a permis de rectifier mes deux messages qui relatent la solution
générale dans et dans
et dans  : j'avais oublier d'écrire le
: j'avais oublier d'écrire le  en facteur de
en facteur de 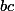 dans
dans 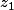 et
et 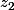 .
.
Merci M.Pseuda pour votre exemple, il m'a permis de rectifier mes deux messages qui relatent la solution
générale dans
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
