limit a + l'infini de
Limite
5 messages
- Page 1 sur 1
Limite
Bonsoir, j'arrive pas de trouver cette limite, c qlq'un peux m'aider s'ils vous plait
limit a + l'infini de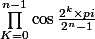
limit a + l'infini de
Re: Limite
Bonjour;
Votre exercice est un cas particulier d'un exercice classique, qui est comme suit :
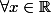 , calculer
, calculer  = \prod_{k=0}^n \cos(2^k x)) .
.
Vous calculez P(x)) en utilisant l'identité trigonométrique :
en utilisant l'identité trigonométrique :  = 2 \sin(a) \cos(a)) , ensuite vous retournez à votre cas particulier dont vous calculerez la limite.
, ensuite vous retournez à votre cas particulier dont vous calculerez la limite.
Bon courage.
Votre exercice est un cas particulier d'un exercice classique, qui est comme suit :
Vous calculez
Bon courage.
Re: Limite
Bonjour,
Mon forfait de connexion risque de s'épuiser à tout instant, donc je donne une dernière indication:
On a pour = \prod_{k=0}^{n-1} \cos(2^k \frac{\pi}{2^n-1}))
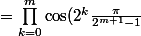 = \frac{1}{2^{m+1}}\frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\sin(\frac{\pi}{2^{m+1}-1})}) .
.
Bon courage .
Mon forfait de connexion risque de s'épuiser à tout instant, donc je donne une dernière indication:
On a pour
Bon courage .
Re: Limite
Bonjour,
pour savoir si ma démarche aboutit au bon résultat et s'il y a d'autres démarches plus simples, je soumets ma solution à discussion.
On a pour = \prod_{k=0}^{n-1} \cos(2^k \frac{\pi}{2^n-1}))
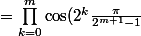 = \frac{1}{2^{m+1}}\frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\sin(\frac{\pi}{2^{m+1}-1})})
De prime abord, on a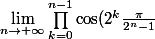) ayant une forme indéterminée :
ayant une forme indéterminée : 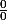 , donc on va essayer de lever l'indétermination.
, donc on va essayer de lever l'indétermination.
On a = (\frac{2^{m+1}\pi}{2^{m+1}-1} - \pi)\frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi} = - \frac{\pi}{2^{m+1}-1} \frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi}) ,
,
donc = - \frac{\pi}{2^{m+1}-1} \frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi}) ,
,
comme on a = \frac{\pi}{2^{m+1}-1}\frac{\sin(\frac{\pi}{2^{m+1}-1})}{\frac{\pi}{2^{m+1}-1}}) ,
,
donc}{\sin(\frac{\pi}{2^{m+1}-1})} = - \frac{\frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi}}{\frac{\sin(\frac{\pi}{2^{m+1}-1})}{\frac{\pi}{2^{m+1}-1}}}) .
.
On a}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi} = \cos(\pi}) = -1) et
et }{\frac{\pi}{2^{m+1}-1}} = 1)
donc}{\sin(\frac{\pi}{2^{m+1}-1})} = \lim_{m \rightarrow + \infty} - \frac{\frac{\sin(2^{m+1}\frac{\pi}{2^{m+1}-1})}{\frac{2^{m+1}\pi}{2^{m+1}-1}-\pi}}{\frac{\sin(\frac{\pi}{2^{m+1}-1})}{\frac{\pi}{2^{m+1}-1}}} = 1) ,
,
et comme
donc = \lim_{m \rightarrow + \infty} \prod_{k=0}^{n-1} \cos(2^k \frac{\pi}{2^n-1})=\lim_{m \rightarrow + \infty} \prod_{k=0}^m \cos(2^k \frac{\pi}{2^{m+1}-1}))
}{\sin(\frac{\pi}{2^{m+1}-1})} = 0) .
.
pour savoir si ma démarche aboutit au bon résultat et s'il y a d'autres démarches plus simples, je soumets ma solution à discussion.
On a pour
De prime abord, on a
On a
donc
comme on a
donc
On a
donc
et comme
donc
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
