Question
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 20:23
par nada-top » 06 Oct 2006, 20:23
[FONT=Palatino Linotype]bonsoir,
comment démontrer en général que la représentation graphique d'une fonction est symétrique par rapport à la 1ère bissectrice ?
Merci [/FONT] :happy3:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 06 Oct 2006, 20:35
par Zebulon » 06 Oct 2006, 20:35
Bonsoir,
toute fonction serait symétrique par rapport à la première bissectrice?
Et la droite d'équation y=x+1, qu'est-ce qu'elle fait?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 20:45
par nada-top » 06 Oct 2006, 20:45
bonsoir,
j'ai pas dit que
toute fonction est symetrique par rapport à la 1ère bessectrice !!
""comment démontrer qu'
une fonction est..""
de toute façon je parle plus précisemment d'une fct bijective de
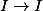
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 06 Oct 2006, 20:55
par Zebulon » 06 Oct 2006, 20:55
OK, il s'agit donc de caractériser ces fonctions. Vous savez ce qu'on doit obtenir ou pas? Parce que moi je trouve une condition nécessaire et suffisante qui n'a pas l'air vraiment exploitable...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 21:02
par nada-top » 06 Oct 2006, 21:02
OK, il s'agit donc de caractériser ces fonctions
ça veut dire quoi caractériser une fonction ?
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 06 Oct 2006, 21:10
par Zebulon » 06 Oct 2006, 21:10
Ca veut dire donner une condition nécessaire et suffisante.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 21:23
par nada-top » 06 Oct 2006, 21:23
ok , je pense qu'il faut prouver que la fct est involutive nan?
-
matteo182
- Membre Relatif
- Messages: 279
- Enregistré le: 01 Mai 2005, 01:14
-
 par matteo182 » 06 Oct 2006, 21:31
par matteo182 » 06 Oct 2006, 21:31
Salut,
Involutive au Lycée ??
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Oct 2006, 21:34
par Flodelarab » 06 Oct 2006, 21:34
décidément, ça te chatouille la
symétrie de la première bissectrice ok , je pense qu'il faut prouver que la fct est involutive nan?
Oui
pour qu'elle soit symétrique, il faut qu'à chaque point (x;y) corresponde son point (y;x) symétrique par rapport à la première bissectrice.
ceci revient a dire: f(f(x))=x
donc f est involutive.
ok?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 21:48
par nada-top » 06 Oct 2006, 21:48
re,
merci encore Flodelarabe ..
ben j'ai calculer f(f(x)) est ça me donne pas x :triste: ..pourtant je suis sure maintenant que ma fonction est symétrique par rapport à la 1ère bissectrice.
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 22:07
par nada-top » 06 Oct 2006, 22:07
ok je trouve :lol5:
enfin fini ce soucis ..
merci
matteo182 a écrit:Salut,
Involutive au Lycée ??
oui.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 06 Oct 2006, 23:20
par Flodelarab » 06 Oct 2006, 23:20
Je suis content que tu n'aies plus de soucis
nada-top a écrit:ben j'ai calculer f(f(x)) est ça me donne pas x :triste: ..pourtant je suis sure maintenant que ma fonction est symétrique par rapport à la 1ère bissectrice.
Ceci pique ma curiosité. Quelle était cette fonction ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 06 Oct 2006, 23:37
par nada-top » 06 Oct 2006, 23:37
ben j'ai honte de le dire :girl2:
c'était tt simplement
^3})
c'est ce

sous la racine carrée :hum: que j'ai oublié en calculant
))
merci
@+
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Oct 2006, 00:47
par Flodelarab » 07 Oct 2006, 00:47
Rien que le fait d'écrire f(f(x)) de façon brute, et de penser que c'est simplement x, m'a fait prendre conscience à quel point les mathématiciens aimaient se faire suer....
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 07 Oct 2006, 09:16
par bdupont » 07 Oct 2006, 09:16
Ami du surréalisme bonjour,
Une fonction symétrique par rapport à la bisectrice? Pigs will fly ...
(A tout x correspondraient 2 y)
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 07 Oct 2006, 10:24
par rene38 » 07 Oct 2006, 10:24
Bonjour
bdupont a écrit:(A tout x correspondraient 2 y)
Mais non, regarde et trace la première bissectrice (en supposant le repère orthonormé) :

-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Oct 2006, 10:49
par Flodelarab » 07 Oct 2006, 10:49
bdupont a écrit:Ami du surréalisme bonjour,
Une fonction symétrique par rapport à la bisectrice? Pigs will fly ...
(A tout x correspondraient 2 y)
bien sur que non.
Je te proposes différentes fonctions prises aux hasard:
f(x)=x
f(x)=-x
f(x)=1/x
.... tente de le représenter et tu verras bien une symétrie.
ok?
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 07 Oct 2006, 18:33
par bdupont » 07 Oct 2006, 18:33
Merci de votre bienveillance car je me suis égaré grave.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités

