Ex noté pour lundi 9/10/06

par **Tzig** » 07 Oct 2006, 17:23

Voilà, là je coince:

"Le triangle de côtés a=3 , b=4 , c=6 n'est pas rectangle. Peut-on, en ajoutant une même longueur x à ses trois côtés, obtenir un triangle rectangle ?"

C'est le chapitre sur le 2nd degré.

J'ai essayé : (3+x)² + (4+x)² = (6+x)² car d'après pythagore, a² + b² = c²...
J'ai developpé, cherché les racines mais cela ne donne rien de concluant...

Quelqu'un peut-il m'aider ??

Merci Bcp d'avance !!

par **Monsieur23** » 07 Oct 2006, 17:28

J'ai essayé : (3+x)² + (4+x)² = (6+x)² car d'après pythagore, a² + b² =c²

Et ça donne quoi ?
En quelle classe es-tu ?

Bon courage,
Mr.23

par **Tzig** » 07 Oct 2006, 17:34

Je suis en 1ere S

2x²-14x+25 = x²-12x-36

Premier membre = pas de racines
2nd membre = 1 seule racine qui est 6.

Merci

par **Flodelarab** » 07 Oct 2006, 17:37

Mets donc tout dans le meme membre et cherches les 0 ...

Pasque si t'attends que les paraboles se croisent pour leur racines, tu peux toujours attendre ....

par **Monsieur23** » 07 Oct 2006, 17:39

Je pense qu'il serait judicieux de tout ramener d'un coté de l'équation, pour avoir une équation de la forme ax²+bx+c=0 ... tu pourras la résoudre :we:

Bon courage,
Mr.23

Edit : /mode Gros Lent ON :triste:

par **Tzig** » 07 Oct 2006, 17:43

Héhé eh ben oui j'y est pensé:

2x²-14x+25 = x²-12x-36

x²-2x+61=0

b²-4ac = (-2)²-4*1*61
=-240
Delta < 0 donc pas de racines...

Me serais-je trompé ? Est-ce la réponse à l'exercice ?

par **Monsieur23** » 07 Oct 2006, 17:47

Hmmm ...
Tu te serais pas trompé dans ton développement ?
(a+b)² = a²+b²+2ab

Je ne vois pas d'où sortent tous les moins...

Bon courage
Mr.23

par **Tzig** » 07 Oct 2006, 17:48

Olalalalala, mais quel ******, bien sûr que je me suis trompé....
Pas malin, je recalcule ca et je reviens !

MErci

par **Tzig** » 07 Oct 2006, 17:59

Bon j'ai refait le developpement :
je trouve x²+2x-11=0

Il y a 2 racines car Delta = 48
x1 = (-2-racine 48)/2 environ egal à -4.46
x2 = (-2+racine 48)/2 environ egal à 2.46

Quelle est alors la réponse à cet exercice si je ne me suis de nouveau pas trompé dans le calcul ?? :cry:

Merci !

par **Monsieur23** » 07 Oct 2006, 18:03

J'avais trouvé ça aussi

Enfin tu peux simplifier par

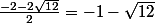
et pareil pour l'autre solution.

Tu peux aussi remarquer qu'une des deux solutions n'est pas compatible avec le problème ( une longueur doit être positive ).

Bravo !

Mr.23

par **Tzig** » 07 Oct 2006, 18:07

Merci beaucoup !!! :++:

Je risque de revenir si j'ai un problème pour le dernier exercice !!

Je te remercie de l'aide que tu m'as apporté !!

par **Flodelarab** » 07 Oct 2006, 18:10

Tzig a écrit:Bon j'ai refait le developpement :
je trouve x²+2x-11=0

Il y a 2 racines car Delta = 48
x1 = (-2-racine 48)/2 environ egal à -4.46
x2 = (-2+racine 48)/2 environ egal à 2.46

Quelle est alors la réponse à cet exercice si je ne me suis de nouveau pas trompé dans le calcul ??

Merci !

Ben si. t'as trouvé la réponse.

Il faut ajouter

à chacun des côtés

Ex noté pour lundi 9/10/06

Ex noté pour lundi 9/10/06

Qui est en ligne