Je cherche à calculer la limite de:
Et je ne vois pas par où commencer, le terme de droite fait penser à une transformée de toeplitz mais comme la série harmonique diverge...
Robot a écrit:Tu ne nous a pas présenté. On peut deviner, mais je n'aime pas jouer aux devinettes.
t.itou29 a écrit:Bonjour,
Je cherche à calculer la limite de:
Et je ne vois pas par où commencer, le terme de droite fait penser à une transformée de toeplitz mais comme la série harmonique diverge...
Matt_01 a écrit:En fait si tu notes S_n la somme (sans le facteur en 2^n) avec les coefficients binomiaux, en utilisant la formule de Pascal, des changements d'indice et en réécrivant correctement (i parmi (n-1)) divisé par (i+1), alors tu peux montrer que S_n=2S_{n-1} +(2^n-1)/n
Dés lors, on montre que la limite qu'on cherche, c'est en fait la somme des 1/(n2^n), qui se calcule très bien avec la bonne série entière évaluée en 1/2.
La méthode que je propose est similaire à celle de M.Matt_01 . Elle repose sur le résultat suivant :
Soientet
deux suites d'éléments de
telles que
, donc
:
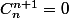
:
.
Ce résultat étant acquis, on aborde tranquillement la problème.
Soientet
deux suites d'éléments de
telles que :
,
et
avec
et
:
, donc
:
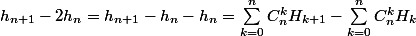
On a aussi
,
donc:
,
donc,
donc}}{n+1})
.
Et comme:
,
donc,
,
donc,
,
donc la suitetelle que
est une suite constante , donc
,
donc:
,
donc.
La série de MacLaurin pourdonne
, donc au point
on a
,
donc,
donc,
donc.
Je suis très content de l'avoir achevé .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :