Partie entière

[Flemme]

Bonjouuur,
Je souffre toujours avec la partie entière ,j'arrive pas à démontrer que :

J'ai montré que :
Et que :
Donc :
Mais sans l'epsilon..?
Et il y a aussi une autre question :
Démontrer que :

Mais je croyais que :
non ?
Franchement je ne sais pas ce que j'ai avec cette partie entière,j'arrive pas à avancer...
Merci de m'aider,merci infiniment pour votre temps!

[nodgim]

E(4,6) + E(5,5) = 4 + 5 = 9
E(4,6 + 5,5) = E(10,1) = 10

Bien voir que la somme de 2 restes peut être supérieure à 1.

Et penser aussi aux nombres négatifs, par exemple dans la seconde question.

[Robot]

Et que :

Quel est ton raisonnement pour montrer ça ?

Démontrer que :

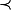
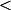
Peux-tu donner l'énoncé exact ? Ce signe , c'est pour ou quoi ?

[aymanemaysae]

Bonsoir,

Pour montrer que avec , on encadre d'abord par et par .

Faîtes cela et ensuite on verra.

[Flemme]

Et que :

Quel est ton raisonnement pour montrer ça ?

Peux-tu donner l'énoncé exact ? Ce signe , c'est pour ou quoi ?

Alors :







Je ne sais pas si c'est juste...
Et pour le signe je me suis trompée,je m'excuse c'est bien :

[Flemme]

Bonsoir,

Pour montrer que avec , on encadre d'abord par et par .

Faîtes cela et ensuite on verra.

Et

Donc:

Et puisque :






C'est faux?

[Robot]

Comment passes-tu de la première ligne à la deuxième ?

[aymanemaysae]

Bonjour,

à mon avis c'est juste, mais on ne peut être sûr que si M. Robot ou l'un des autres professeurs atteste la véracité de cette démarche.

[zygomatique]

salut

si Robot pose la question, ce n'est pas en vain ...

E(x + y) - x =< y => E[E(x + y) - x] =< E(y) car la fonction partie entière est croissante ...

donc la question est : E(x + y) - x est-il un entier ? (et donc égal à sa partie entière)


et donc revenir à la définition de base :




ajouter membre à membre ... et réfléchir ... en remarquant que ...

[Robot]

à mon avis c'est juste, mais on ne peut être sûr que si M. Robot ou l'un des autres professeurs atteste la véracité de cette démarche.

Drôle de méthode de démonstration ! C'est vrai parce que untel me l'a dit !

[aymanemaysae]

Bonjour;

Je parlais de la démonstration citée dans le message suivant: s'il y en a des fautes, je jure que je ça me dépasse.

Bonsoir,

Pour montrer que avec , on encadre d'abord par et par .

Faîtes cela et ensuite on verra.

Et

Donc:
, je crois que jusqu'ici c'est juste.
Et puisque :
, car
, vu que

, vu que


C'est faux?

C'est vrai l'autre méthode est plus claire, mais celle-ci est soit juste soit elle recèle des fautes qui passent à mon insu.
De toute façon, un grand Merci pour l'intérêt que vous avez porté à mes propos.

[Pseuda]

à mon avis c'est juste, mais on ne peut être sûr que si M. Robot ou l'un des autres professeurs atteste la véracité de cette démarche.

Drôle de méthode de démonstration ! C'est vrai parce que untel me l'a dit !

M. aymanemaysae devra attendre que M. Robot (ou l'un des autres professeurs) lui atteste la véracité de la démarche pour la résolution de l'équation du 1er degré, pour en être convaincu.

[aymanemaysae]

Bonjour;

C'est pas que je fais le naïf, mais je suis capable du meilleur comme je suis capable du pire : par chance, çà ne m'arrive pas aux examens.

Quoi que vous dîtes, je vous dois énormément: beaucoup d'astuces que j'ai appris sur ce site m'ont aidé à avoir mon CNC (version marocaine) sans passer par les oraux, comme je viens d'avoir l'ENSMR (Ecole des Mines de Rabat).

Un Grand Merci à Maths-forum.

[Flemme]

Comment passes-tu de la première ligne à la deuxième ?

Je vais pas vous mentir,je l'ai fait au hasard parce que ça me semblait logique (j'ai donné des chiffres à x et y pour vérifier..)
S'il vous plait,ne soyez pas dur avec moi.

[Robot]

N'écris jamais des trucs au hasard, si tu veux qu'on te prenne au sérieux.

[Flemme]

N'écris jamais des trucs au hasard, si tu veux qu'on te prenne au sérieux.

D'accord,merci pour le conseil.Sinon,pouvez vous me montrer mes erreurs? et des liens ou des conseils pour que je comprenne mieux? S'il vous plait (je n'ai pas cette leçon dans mon cahier de cours,je suis entrain de ramasser des informations un peu de partout...)

[Robot]

Ton erreur, c'est d'écrire quelque chose au hasard qui a vaguement l'air d'un raisonnement alors que tu n'as aucun argument pour le justifier.

Je te donne un contre-exemple : . A-t-on ?

[Flemme]

Ton erreur, c'est d'écrire quelque chose au hasard qui a vaguement l'air d'un raisonnement alors que tu n'as aucun argument pour le justifier.

Je te donne un contre-exemple : . A-t-on ?

Non,c'est vrai..Je fais quoi alors ?!!

[Robot]

Tu réfléchis et tu écris un raisonnement dont tu es sûr des arguments.

[Pseuda]

Bonsoir,

Comme dit zygomatique, revenir à la définition de base :




et ajouter membre à membre,

puis utiliser le fait que la partie entière de x+y, soit E(x+y), est, par définition, le plus grand entier inférieur ou égal à x+y. Donc E(x+y) est plus grand que quel autre entier ?

Continue ensuite avec les inégalités, en réfléchissant bien à ce que veut dire cette phrase : "le plus grand entier inférieur ou égal" ; cela veut dire que l'entier qui suit est quant à lui.... le plus petit entier strictement supérieur.