La partie entière

[Flemme]

Bonsoir,
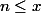
La partie entière est le plus grand nombre entier relatif n tel que , ça veut dire quoi? Pouvez vous me donner des exemples s'il vous plait? On dit le plus "grand nombre" mais on prend le petit?!!! exemple :
-2.3 , E(x)= -3 , -3 est plus petit que -2.3 non?!!
J'ai vu aussi dans un livre un exemple que j'ai pas compris :

Pourquoi?
Avez-vous des conseils ou des exercices pour que je comprenne mieux s'il vous plait?
Merci infiniment!

[Razes]

Bonsoir,
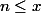
La partie entière est le plus grand nombre entier relatif n tel que , ça veut dire quoi? Pouvez vous me donner des exemples s'il vous plait? On dit le plus "grand nombre" mais on prend le petit?!!! exemple :
-2.3 , E(x)= -3 , -3 est plus petit que -2.3 non?!!
J'ai vu aussi dans un livre un exemple que j'ai pas compris :

Pourquoi?
Avez-vous des conseils ou des exercices pour que je comprenne mieux s'il vous plait?
Merci infiniment!

Oui
Quel livre?

[Flemme]

Bonsoir,
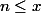
La partie entière est le plus grand nombre entier relatif n tel que , ça veut dire quoi? Pouvez vous me donner des exemples s'il vous plait? On dit le plus "grand nombre" mais on prend le petit?!!! exemple :
-2.3 , E(x)= -3 , -3 est plus petit que -2.3 non?!!
J'ai vu aussi dans un livre un exemple que j'ai pas compris :

Pourquoi?
Avez-vous des conseils ou des exercices pour que je comprenne mieux s'il vous plait?
Merci infiniment!

Oui
Quel livre?

Alors pourquoi on dit le plus "grand nombre" si on prend -3 ??!!
C'est un livre arabe.(التحليل الرياضي)

[Razes]

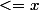
C'est le plus grand nombre de plus tu es dans la partie des nombre négatifs.

Tu peux tracer un axe avec les nombre entiers relatifs, La partie entière d'un nombre x est son voisin à sa gauche sur l'axe.

[Razes]

C'est un livre arabe.(التحليل الرياضي)

Je n'ai pas ce livre. Tu n'as pas changé ton pseudo?

[Flemme]

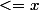
C'est le plus grand nombre de plus tu es dans la partie des nombre négatifs.

Tu peux tracer un axe avec les nombre entiers relatifs, La partie entière d'un nombre x est son voisin à sa gauche sur l'axe.

J'ai pas compris!!
Oui,je suis dans la partie des nombres négatifs,on a par exemple -4.5 ,on dit que la partie entière est le plus grand nombre entier relatif,alors pourquoi on ne prends pas -4 ? -4 est plus grand que -5! En fait le x il représente quoi? Et pour l'autre exemple ? Je ne comprends paaaaas!

C'est un livre arabe.(التحليل الرياضي)

Je n'ai pas ce livre. Tu n'as pas changé ton pseudo?

Non,je le changerai quand je passerai en 2eme .(nchallah)

[Razes]

Soit x=-4.5
Les nombres entiers relatifs inférieurs ou égale à x sont (il y en a une infinité) ..............
La partie entière correspond au plus grand de ces nombre. (fais un essais)

[Flemme]

Soit x=-4.5
Les nombres entiers relatifs inférieurs ou égale à x sont (il y en a une infinité) ..............
La partie entière correspond au plus grand de ces nombre. (fais un essais)

C'est boooon,j'ai compris merciii!!
Et pour l'autre exemple?

[Razes]

Quel exemple?

[Flemme]

Quel exemple?

Celui là :

[Razes]

Fais un effort, maintenant que les choses sont claires pour toi.

[Sake]

Salut Flemme,

Tu sais que pour un x réel donné, E(x) est donné par E(x) < x ≤ E(x) + 1

Donc n + E(x) < n + x

Pourtant, tu sais aussi que E(n + x) est le plus petit entier inférieur à n + x...

Je te laisse terminer.

[Black Jack]

Salut Flemme,

Tu sais que pour un x réel donné, E(x) est donné par E(x) < x ≤ E(x) + 1

Donc n + E(x) < n + x

Pourtant, tu sais aussi que E(n + x) est le plus petit entier inférieur à n + x...

Je te laisse terminer.

En-es-tu bien sûr(e) ?
Pour x = 5 par exemple.

[aymanemaysae]

Bonjour;

On a pour ,

donc .

[Flemme]

Merci beaucoup. ^^

[Sake]

Salut Flemme,

Tu sais que pour un x réel donné, E(x) est donné par E(x) < x ≤ E(x) + 1

Donc n + E(x) < n + x

Pourtant, tu sais aussi que E(n + x) est le plus petit entier inférieur à n + x...

Je te laisse terminer.

En-es-tu bien sûr(e) ?
Pour x = 5 par exemple.

Une petite coquille de ma part sur les inégalités strictes ou pas, bien entendu.

[Robot]

tu sais aussi que E(n + x) est le plus petit entier inférieur à n + x...

J'ai beau chercher le plus petit entier relatif inférieur à n+x, j'en trouve toujours un plus petit ...