et j'aimerais qu'on puisse m'expliquer quelle formule on a utilisée et les étapes pour arriver aux différents résultats :sIntégrale définie
8 messages
- Page 1 sur 1
intégrale définie
par clard » 21 Juil 2016, 11:51
Bonjour, me revoilà avec un tout autre problème: voici un exercie sin(x)*dx} \Rightarrow [-\frac{1}{3}cos^3(x)]^\frac{\Pi }{3} indice en dessous \frac{\Pi }{4} = \frac{1}{24}(-1+\sqrt[2]{2}))
je comprend pas du tout cet exemple là et j'aimerais qu'on puisse m'expliquer quelle formule on a utilisée et les étapes pour arriver aux différents résultats :s
et j'aimerais qu'on puisse m'expliquer quelle formule on a utilisée et les étapes pour arriver aux différents résultats :sRe: intégrale définie
par aymanemaysae » 21 Juil 2016, 13:02
Bonjour,
On a \cos^2(x) = -\frac{1}{3} (-3 \sin(x) \cos^2(x)) = -\frac{1}{3} (3 (-\sin(x)) \cos^2(x)))
)' \cos^2(x)) = -\frac{1}{3} (\cos^3(x))')
,
donc \cos^2(x) dx = -\frac{1}{3} \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} (\cos^3(x))' dx =-\frac{1}{3} [\cos^3(x)]_{\frac{\pi}{4}}^{\frac{\pi}{3}}= -\frac{1}{3} ((\frac{1}{2})^3 - (\frac{\sqrt 2}{2})^3))
 = \frac{1}{24} (2\sqrt 2 - 1))
.
J'espère que c'est clair maintenant .
On a
donc
J'espère que c'est clair maintenant .
Re: intégrale définie
par clard » 21 Juil 2016, 14:00
merci de la réponse je vois déjà plus clair 
mais il me reste des incompréhensions
d'ou vient ce fameux -1/3
ou va le 3 de (3(cos(x))'
et je comprend pas comment on arrive a 1/2 et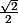
mais il me reste des incompréhensions d'ou vient ce fameux -1/3
ou va le 3 de (3(cos(x))'
et je comprend pas comment on arrive a 1/2 et
Re: intégrale définie
par aymanemaysae » 21 Juil 2016, 14:15
Bonjour,
Tout d'abord on a : = \frac{1}{2})
et  = \frac{\sqrt 2}{2})
,
et en ce qui concerne le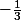
on a divisé par 
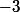et multiplié par 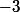, donc on a procédé comme si on a multiplié par 
, et ceci pour faire apparaître le 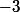à côté de  \cos^2(x))
pour avoir  \cos^2(x))
qui est la dérivée de )
.
clard a écrit:merci de la réponse je vois déjà plus clair
d'ou vient ce fameux -1/3
ou va le 3 de (3(cos(x))'
et je comprend pas comment on arrive a 1/2 et
Tout d'abord on a :
et en ce qui concerne le
Re: intégrale définie
par zygomatique » 21 Juil 2016, 14:18
salut
et si tu prenais un crayon et un papier pour te mettre au travail sérieusement ?
quelle est la dérivée de]^n)
?
quelle est donc une primitive de [u(x)]^n)
?
ensuite peut-être connaître les valeurs particulières associées aux fonctions cos et sin ...
et si tu prenais un crayon et un papier pour te mettre au travail sérieusement ?
quelle est la dérivée de
quelle est donc une primitive de
ensuite peut-être connaître les valeurs particulières associées aux fonctions cos et sin ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: intégrale définie
par Lostounet » 21 Juil 2016, 16:04
Au pire les formules d'Euler permettent de se ramener à des gentilles exp:
 = \frac{e^{ix} + e^{-ix}}{2})
 = \frac{e^{ix} - e^{-ix}}{2i})
Donc, = cos^2(x)sin(x) = -1/8 i (-e^{-3 i x}+e^{3 i x}+2 i sin(x)))
Donc,
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: intégrale définie
par Black Jack » 23 Juil 2016, 09:03
cos²(x).sin(x) est de la forme -u²*u' (avec u = cos(x))
Une primitive est donc -u³/3 ... soit donc -cos³(x)/3
Une primitive est donc -u³/3 ... soit donc -cos³(x)/3
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :