Suites 1ère S

[xsKyx]

Bonjour ou bonsoir selon l'heure à laquelle vous lisez ce message . J'aurais besoin d'aide si possible sur un exercice de suites:
On considère la suite (Vn)n>ou= à 0 définie sur N par: Vn=Un-1/Un+2
a. Calculer V0, V1 et V2
Je ne me suis pas encore penchée sur les trois autres questions mais ça n'a l'air pas compliquer puis j'ai une autre question que je ne comprends pas en rapport avec l'exercice qui est:
Conjecturer le comportement des termes Un lorsque n devient très grand. Que veut dire réellement conjecturer ?
Pour ceux qui pourront m'aider merci d'avance !

[Eliza]

Qu'est (Un) ?

[xsKyx]

Un est le terme d'incide n de la suite.

[WillyCagnes]

peut-être le même exo que
lycee/resolution-equation-t175331.html

sinon V0=[U0-1]/[U0+2]
V1=[U1-1]/[U1+2]
V2=[U2-1]/[U2+2]

[xsKyx]

Absolument pas WillyCagnes

[WillyCagnes]

Vn=(Un-1)/(Un+2)=(Un+2 -3)/(Un+2)= 1-3/(Un+2)
si Un devient très grand alors Vn tend vers 1

[xsKyx]

Cela correspond à V0 ? WillyCagnes

[Razes]

Sans parenthèses, ça brouille l'énoncé. Est ce ça ta suite ?

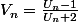
[xsKyx]

Oui c'est ma suite

[Razes]

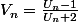
L'énoncé me semble embrouillé et incomplet. Il y a deux suites et avec la relation et que

A la limite tu peux étudier la fonction

[Razes]

Tu pourrais poster l'énoncé complet non modifié?

[xsKyx]

Je te donner l'énoncé en complet alors:
On considère la suite (Un)n>0 définie par:
u0=3
un+1=2/1+un

1) Calculer u1 et u2. La suite est-elle arithmétique?Géométrique?
2)a.Déterminer une fonction f telle que un+1=f(un)
b.Résoudre dans R\{-1} l'équation f(x)=x
3)On considère la suite (Vn)n>ou= à 0 définie sur N par: Vn=Un-1/Un+2
a. Calculer V0, V1 et V2
b.Démontrer que la suite (Vn)n>0 est géométrique.
c.Exprimer pour tout entier naturel n, vn en fonction de n.
d.En déduire, pour tout entier naturel n , un en fonction de n.
4)Conjecturer le comportement des termes un lorsque n devient très grand.

[Razes]

Là c'est mieux, il y a aussi la relation

Visite le lien suivant

http://www.maths-forum.com/superieur/suite-recurrente-coriace-t175383.html

, C'est un cas traité hier. Si tu n y arrive pas, je t'aiderais.

[Razes]

Je te donner l'énoncé en complet alors:
On considère la suite (Un)n>0 définie par:
u0=3
un+1=2/1+un

1) Calculer u1 et u2. La suite est-elle arithmétique?Géométrique?
2)a.Déterminer une fonction f telle que un+1=f(un)
b.Résoudre dans R\{-1} l'équation f(x)=x
3)On considère la suite (Vn)n>ou= à 0 définie sur N par: Vn=Un-1/Un+2
a. Calculer V0, V1 et V2
b.Démontrer que la suite (Vn)n>0 est géométrique.
c.Exprimer pour tout entier naturel n, vn en fonction de n.
d.En déduire, pour tout entier naturel n , un en fonction de n.
4)Conjecturer le comportement des termes un lorsque n devient très grand.

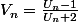
Donc : Remplace par son expression en fonction de . Quelle relation lie et ?

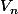
[xsKyx]

Je remplace du genre V0+1=U0+1-1/U0+1+2?

[Razes]

Je remplace du genre V0+1=U0+1-1/U0+1+2?

Non, plutôt les expressions avec indices n. Essais de mettre des parenthèses pour que ce soit lisible.

[Razes]

As tu visité la page suivante de ce forum? http://www.maths-forum.com/superieur/suite-recurrente-coriace-t175383.html

[xsKyx]

Oui mais je comprend rien ça m'énerve j'ai l'impression d'être une merde

[Eliza]

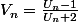
Donc : Remplace par son expression en fonction de . Quelle relation lie et ?

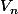
Réinjecte l'expression de en fonction de : dans celle de . Alors on a la relation entre et .

[xsKyx]

J'ai trouvé que V1 était égal à 0 ce n'est pas normal.