Problème (intégrale, limites)

[Okamyne]

Bonsoir,j'ai joint ici quelques question en eperant votre aide merci.

[WillyCagnes]

1)I=e(x)[sinx -cosx] +Cte

[samoufar]

Bonjour,

Je te donnes quelques indications (puisque ça semble être un QCM ) :

Question 6 : Si je fais une intégration par partie, je me retrouve avec du cosinus dans l'intégrale. Mais si j'intègre par partie une deuxième fois, que se passe-t-il ?

Question 7 : Classique, l'égalité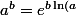 devrait donner quelque chose.

Question 8 : Une propriété sympathique du logarithme en ce qui concerne les puissances devrait grandement simplifier la fonction .

Question 9 : Au numérateur, on a une somme. Quel terme serait négligeable devant l'autre à l'infini ?

[Okamyne]

Merci, alors voila pour la deuxième j'ai trouvé la réponce D, la troisième : D aussi, mais pour la première et dernière je ne vois pas vraiment, pouvez vous m'éclairer la dessus ?

[samoufar]

Tes réponses sont correctes

Pour la dernière, une autre façon de faire serait simplement de séparer ta somme en deux :



Il reste à simplifier ce qui est simplifiable et à voir ce qu'on peut en faire

[Okamyne]

Merci encore, en simplifiant je trouve la réponce D, ( dans le cas ou n est pair ou impaire la limite égale à zero). Pour ce qui est du premier intégrale, en faisant une intégration par partie deux fois je retombe sur l'intégrale je ne sais pas quoi faire aprés.

[WillyCagnes]

bjr

tu poses U=sinx et V=exp(x)
U'=cosx.dx
V'=exp(x)dx

integration par partie

I1 = 2int(UdV) = 2UV -2int(VdU) = 2sin(x)exp(x) -2int(VdU)

or -2 int(VdU) = -2int(exp(x)cos(x)dx
=-2 [exp(x)cos(x)- int(exp(x)(-sin(x)) dx]
= -2exp(x)cos(x) -2int(exp(x)sin(x)dx que je reporte dans I1

I1= 2sin(x)exp(x)-2 [exp(x)cos(x) -I1

soit 2I1=2exp(x)[sin(x) -cos(x)]

donc I1=exp(x)[sin(x)- cos(x)] +Cte
tu rentres les bornes[0,Pi] et
I1=1+e(pi)

[Calvinator2000]

Bonjour, je crois que l'intégration par parties n'est plus au programme de Terminale S.

Du coup je te propose ceci :



En remplaçant dans l'intégrale qu'obtiens-tu ?

[WillyCagnes]

bjr,

attention au complexe
e(ix)=cosx +isinx different de e(x)

[Calvinator2000]

Autant pour moi, j'ai modifié, mais aucune réponse de l'auteur.