J'aurais besoin d'aide pour résoudre une éq diff, je ne sais pas trop comment m'y prendre. Théta et r dépendent de t. Est-ce possible d'obtenir quelque chose comme théta en fonction de r et t ?
Equation différentielle compliquée
11 messages
- Page 1 sur 1
Equation différentielle compliquée
Bonjour,
J'aurais besoin d'aide pour résoudre une éq diff, je ne sais pas trop comment m'y prendre. Théta et r dépendent de t. Est-ce possible d'obtenir quelque chose comme théta en fonction de r et t ?
=0)
J'aurais besoin d'aide pour résoudre une éq diff, je ne sais pas trop comment m'y prendre. Théta et r dépendent de t. Est-ce possible d'obtenir quelque chose comme théta en fonction de r et t ?
Re: Equation différentielle compliquée
salut
on ne te répondra pas mieux que dans le supérieur ...
superieur/equation-differentielle-compliquee-t175165.html
...
on ne te répondra pas mieux que dans le supérieur ...
superieur/equation-differentielle-compliquee-t175165.html
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Equation différentielle compliquée
bjr
tu remplaces sin(théta) par l'angle théta (une approximation aux ptits angles, ensuite tu devrais savoir résoudre l'equation
es-tu sûr de la dérivée 1ère au carré?
tu remplaces sin(théta) par l'angle théta (une approximation aux ptits angles, ensuite tu devrais savoir résoudre l'equation
es-tu sûr de la dérivée 1ère au carré?
Re: Equation différentielle compliquée
Oui il y a bien un carré et théta peut varier de 0 à pi/2 donc je ne crois pas pouvoir écrire theta=sin(theta)
Re: Equation différentielle compliquée
Bonjour, l'équation que tu donnes n'est pas résoluble analytiquement avec les fonctions classiques. On peut exprimer la solution via les fonctions de Jacobi mais pour que ce soit utile il faut que r(t) soit suffisamment simple.
Sinon, avec les notations on a très envie de conclure que tu essayes de décrire un pendule pesant de longueur variable, mais dans ce cas il y a probablement une erreur dans ton équa diff... Prends l'habitude de décrire la totalité de ton problème, quitte à poster dans le forum physique.
Sinon, avec les notations on a très envie de conclure que tu essayes de décrire un pendule pesant de longueur variable, mais dans ce cas il y a probablement une erreur dans ton équa diff... Prends l'habitude de décrire la totalité de ton problème, quitte à poster dans le forum physique.
Re: Equation différentielle compliquée
Salut, merci de ta réponse. En fait l'exo c'est déterminer les équations du mouvement d'un projectile lancé sur Terre en polaire. (je l'ai d'abord fait en cartésien ce qui marche assez bien car le poids est selon un axe)
Mais là du coup en polaire ça me donne ça :
\vec{u_{\rho}}-g.cos(\theta)\vec{u_{\theta}})
et en polaire (la vitesse étant toujours selon +- ) j'ai trouvé :
) j'ai trouvé :

\vec{u_{\theta}})
Par identification sur la composante rho, on retrouve l'eq diff post 1 :
=0)
Mais là du coup en polaire ça me donne ça :
et en polaire (la vitesse étant toujours selon +-
Par identification sur la composante rho, on retrouve l'eq diff post 1 :
Re: Equation différentielle compliquée
Tu n'as pas bien calculé la vitesse et l'accélération :

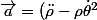\vec{u_{\rho}}+(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{u_{\theta}})
Au final tu vas tomber sur un système bien compliqué, dont la résolution analytique va passer par un changement de variables pour retourner en cartésiennes...
Au final tu vas tomber sur un système bien compliqué, dont la résolution analytique va passer par un changement de variables pour retourner en cartésiennes...
Re: Equation différentielle compliquée
Ah ok, j'avais bien calculé mais j'avais considéré à tort que v était selon u théta mais oui ce n'est pas le cas ^^. Du coup par le polaire on tombe régulièrement sur un système compliqué à ce que je vois...
Re: Equation différentielle compliquée
C'est toujours plus simple de se placer dans un référentiel adapté au problème. Si ton problème est "naturellement" cartésien comme ici, tu peux être certain de te compliquer la vie en passant en polaires. Face à un problème "naturellement" polaire (genre force centrale) ben c'est le contraire.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
