équation 2nd

par **zouzaline** » 06 Oct 2006, 17:26

voilà j'ai une équation a résoudre mais je vois vrémen pas comment il faut faire donk si kelkun pourrai m'aider...se serait sympas! :we:

Soient a et b deux nombres réels strictements positif.

1)Montrer que: "racine carré de" b - "racine carré de" a = (b-a) divisé par "racine carré de" b + "racine carré de" a.

2) en déduir ke si a inférieur ou égale à b, alors "racine carré de" a inférieur ou égale à "racine carré de" b.

voilà merci d'avance! :hein: :we:

par **Imod** » 06 Oct 2006, 17:32

Pour la première question , calcule :

. Pour la deuxième question tu dois pouvoir te débrouiller tout seul .

Imod

par **zouzaline** » 06 Oct 2006, 17:35

ok merci mais je vois pas pourkoi faire ("racine carré de" b - "racine carré de" a)("racine carré de" b + "racine carré de" a)... c koi le rapport? :hein:

par **Zebulon** » 06 Oct 2006, 17:37

Bonsoir,
pour la première question, on regarde ce que signifie que

.
Ceci est équivalent à

.
Autrement dit :
si

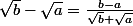
est vraie alors

est vraie
et si

est vraie alors

est vraie.
Mais, à votre avis, est-ce qu'il est vrai que

? Si oui, c'est gagné!

par **Imod** » 06 Oct 2006, 17:40

Essaie d'imaginer ce qu'il peut bien avoir dans les points de suspensions .

.

Imod

par **zouzaline** » 06 Oct 2006, 17:41

ok merci g compris :id: !! et on me demande "énoncer le théorème ainsi démontré" et...j'voi pas! :triste:

par **Imod** » 06 Oct 2006, 17:49

Essaie de traduire ton 2) en terme de fonction .

Imod

par **zouzaline** » 06 Oct 2006, 18:02

ah wé c vrai pour le théorème j'ai pas fait attention!! Mais zébulon ta di ke si (racine carré de b - racine carré de a)(racine carré de b + racine carré de a)=b - a , alors c bon...mé si c pas égal? ( parceke (racine carré de b - racine carré de a)(racine carré de b + racine carré de a) = b² - a² non? et b²-a² n'est pas égale à b-a... :hein: )

par **Zebulon** » 06 Oct 2006, 18:13

Vous avez raison, si

, alors

.
Mais je prétends que c'est égal et donc que c'est vrai!
Oubliez ma démonstration car en seconde on ne connaît pas vraiment les équivalences et reprenez plutôt celle proposée par Imod (avec les points de suspension).

par **zouzaline** » 06 Oct 2006, 18:24

ok merci! :++: :we:

par **zouzaline** » 06 Oct 2006, 18:29

ah non j'croi ke c bon pour (racine carré de b - racine carré de a)(racine carré de b+racine carré de a) = b-a puiske (racine carré de b)²=b !

donk je croi ke c bon!

par **Zebulon** » 06 Oct 2006, 18:31

Oui, bien sûr que ça marche, mais je pense que la méthode de Imod est plus adaptée au niveau de seconde. Il faut utiliser le fait que :
on peut multiplier une fraction "en haut et en bas", ça ne change pas le résultat.

par **zouzaline** » 06 Oct 2006, 19:16

é pour "en déduire que si a inférieur ou égal à b alors 'racine carré de' a inférieure ou égale à 'racine carré de' b"???

j'vois pas comment l'expliquer! :hein:

par **Imod** » 06 Oct 2006, 20:07

x > y est équivalent à x-y > 0 .

Pour la dernière question , pense que la racine est une fonction , reprends ta propriété en mettant f à la place de racine et ça devrait te rappeler quelque chose .

Imod

équation 2nd

équation 2nd

Qui est en ligne