Bonjour
je cherche un contre exemple pour montrer qu un groupe abelien G n est pas toujours isomorphe a G\H*H
H un sous groupe de G
Merci pour votre aide
Theorie des groupe
12 messages
- Page 1 sur 1
Re: theorie des groupe
Indice : le plus petit contre-exemple est d'ordre 4. (Il n'y a pas beaucoup de groupes d'ordre 4 à isomorphisme près - peux-tu en faire la liste ?)
Re: theorie des groupe
dans mon cours j'ai étudié qu il y a 2 cas possibles de groupe d ordre 4
les groupes de Klein dont tous les éléments sont d ordre inférieure ou égale a 2 isomorphe a Z/2Z * Z/2Z
et les groupes cycliques isomorphe Z/4Z
Merci
les groupes de Klein dont tous les éléments sont d ordre inférieure ou égale a 2 isomorphe a Z/2Z * Z/2Z
et les groupes cycliques isomorphe Z/4Z
Merci
Re: theorie des groupe
Alors, as-tu trouvé le G d'ordre 4 et son sous-groupe H qui fournissent le contre-exemple demandé ?
Re: theorie des groupes
Ce n'est pourtant pas difficile de regarder ce qui se passe pour les groupes d'ordre 4. Un p'tit effort !
Re: theorie des groupe
Houuda a écrit:Bonjour
je cherche un contre exemple pour montrer qu un groupe abelien G n est pas toujours isomorphe a G\H*H
H un sous groupe de G
Merci pour votre aide
Bonjour;
ça fait plus de cinq jours que j'attends en vain le dénouement de cet exercice, et cela pour la seule raison pour savoir comment on manie et on manipule un tel groupe: G\H * H .
Ce qui m'intrigue c'est que G\H est le groupe quotient , H un sous groupe de G, et si j'ai bien compris G\H * H est le produit cartésien de G\H et H qu'on a muni d'une certaine loi de composition interne qui lui confère le statut de groupe.
Si quelqu'un peut éclairer ma lanterne, je le remercierai amplement.
Re: theorie des groupe
C'est bien entendu G/H et non G\H qu'il faut écrire.
J'ai donné tout ce qu'il faut pour s'en sortir, si on se prend par la main : un contre-exemple se cache parmi les groupes d'ordre 4. Houuda en a fait la liste, elle est bien courte.
Un groupe d'ordre 4 peut avoir des sous-groupes d'ordre 1, 2 ou 4. On n'aura pas de contre-exemple avec le sous-groupe d'ordre 1 (ne contenant que l'élément neutre) ni avec le sous-groupe d'ordre 4 (le groupe tout entier). Il faut donc regarder les sous-groupes d'ordre 2. Combien y en a-t-il pour chacun des groupes de la liste de Houuda ?
On n'a pas beaucoup de choix pour la structure du quotient d'un groupe d'ordre 4 par un sous-groupe d'ordre 2.
Partant de là, le contre-exemple se trouve facilement, pourvu qu'on réfléchisse un tout petit peu !
J'ai donné tout ce qu'il faut pour s'en sortir, si on se prend par la main : un contre-exemple se cache parmi les groupes d'ordre 4. Houuda en a fait la liste, elle est bien courte.
Un groupe d'ordre 4 peut avoir des sous-groupes d'ordre 1, 2 ou 4. On n'aura pas de contre-exemple avec le sous-groupe d'ordre 1 (ne contenant que l'élément neutre) ni avec le sous-groupe d'ordre 4 (le groupe tout entier). Il faut donc regarder les sous-groupes d'ordre 2. Combien y en a-t-il pour chacun des groupes de la liste de Houuda ?
On n'a pas beaucoup de choix pour la structure du quotient d'un groupe d'ordre 4 par un sous-groupe d'ordre 2.
Partant de là, le contre-exemple se trouve facilement, pourvu qu'on réfléchisse un tout petit peu !
Re: theorie des groupe
Bonsoir;
Je voudrai d'abord vous remercier pour votre patience et votre indulgence.
Ensuite, je récapitule ce qui a été dit dans cette discussion:
1) Le groupe en question est le groupe de Klein, qui est un groupe abélien, isomorphe à ℤ/2ℤ × ℤ/2ℤ.
Ce groupe peut être symbolisé par la lettre G, et donc on a G = { e(élément neutre du groupe),a,b,c } avec pour table de Cayley la table suivante (en prenant la loi additive « + » pour loi de composition interne du groupe) :
+ e a b c
e e a b c
a a e c b
b b c e a
c c b a e
Le groupe de Klein est d'ordre 4 , dont tous les éléments hormis l'élément neutre sont d'ordre 2 , et chaque élément est son propre symétrique.
Les sous groupes de G sont :
* les groupes triviaux {e} et G .
* les groupes propres d'ordre 2 : {e,a}, {e,b} et {e,c} .
J'ajoute, qu'en prenant H={e,a} , on a G/H = {{e,a},{b,c}} .
Mais si ce n'est pas trop demander, je n'arrive pas encore à me représenter le groupe G/H*H que Mlle Houda a présenté dans son énoncé: un groupe qu'on obtient par le produit cartésien d'un groupe quotient et d'un sous groupe d'un groupe de départ.
Excusez mon ignorance, mais ce sera un groupe que je n'ai pas vu avant.
Merci .
Je voudrai d'abord vous remercier pour votre patience et votre indulgence.
Ensuite, je récapitule ce qui a été dit dans cette discussion:
1) Le groupe en question est le groupe de Klein, qui est un groupe abélien, isomorphe à ℤ/2ℤ × ℤ/2ℤ.
Ce groupe peut être symbolisé par la lettre G, et donc on a G = { e(élément neutre du groupe),a,b,c } avec pour table de Cayley la table suivante (en prenant la loi additive « + » pour loi de composition interne du groupe) :
+ e a b c
e e a b c
a a e c b
b b c e a
c c b a e
Le groupe de Klein est d'ordre 4 , dont tous les éléments hormis l'élément neutre sont d'ordre 2 , et chaque élément est son propre symétrique.
Les sous groupes de G sont :
* les groupes triviaux {e} et G .
* les groupes propres d'ordre 2 : {e,a}, {e,b} et {e,c} .
J'ajoute, qu'en prenant H={e,a} , on a G/H = {{e,a},{b,c}} .
Mais si ce n'est pas trop demander, je n'arrive pas encore à me représenter le groupe G/H*H que Mlle Houda a présenté dans son énoncé: un groupe qu'on obtient par le produit cartésien d'un groupe quotient et d'un sous groupe d'un groupe de départ.
Excusez mon ignorance, mais ce sera un groupe que je n'ai pas vu avant.
Merci .
Modifié en dernier par aymanemaysae le 14 Juin 2016, 00:05, modifié 1 fois.
Re: theorie des groupe
Le produit cartésien de deux groupes a une structure naturelle de groupe.
Si et
et  sont deux groupes, leur produit cartésien
sont deux groupes, leur produit cartésien  est l'ensemble des couples
est l'ensemble des couples ) où
où 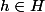 et
et 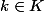 , avec la loi de composition
, avec la loi de composition (h',k')=(hh',kk')) .
.
Une chose m'étonne : tu dis ne pas savoir ce qu'est un produit de groupes, mais tu écris sans problème (avec tout de même un intrus "f" dans la table que tu écris)... Bizarre bizarre.
sans problème (avec tout de même un intrus "f" dans la table que tu écris)... Bizarre bizarre.
Si
Une chose m'étonne : tu dis ne pas savoir ce qu'est un produit de groupes, mais tu écris
Re: theorie des groupe
Bonsoir;
Merci pour l'intérêt que vous avez porté à mon intervention, et je vous suis très reconnaissant car en quelques lignes vous avez pu mettre beaucoup d'ordre dans mes idées: avant vos explications, je savais que le produit cartésien pouvait avoir une structure de groupe, mais une certitude qui s'est implantée dans ma tête et qui refusait de me laisser concevoir un produit cartésien entre un groupe quotient et un sous groupe d'un groupe donné, me disait sans cesse que j'allais faire des produits erronés entre des classes d'équivalence éléments de G/H et des éléments de H, alors qu'en réalité, la loi induite sur G/H*H faisait des produits entre des classes d'équivalences d'un côté et des éléments de H de l'autre.
Je m'excuse pour ce désagrément, et je vous remercie amplement: ce genre de raisonnement irraisonnable m'a créé beaucoup d'ennuis avec mes professeurs depuis le collège, mais je vous demande à vous et aux autres professeurs du site d'être indulgents et magnanime.
Une dernière chose, le "f" que vous avez remarqué est un petit poisson qui a passé entre les mailles d'un copier-coller, quand j'ai rédigé mon intervention: je le corrigerai tout de suite.
Encore une fois, Merci.
Merci pour l'intérêt que vous avez porté à mon intervention, et je vous suis très reconnaissant car en quelques lignes vous avez pu mettre beaucoup d'ordre dans mes idées: avant vos explications, je savais que le produit cartésien pouvait avoir une structure de groupe, mais une certitude qui s'est implantée dans ma tête et qui refusait de me laisser concevoir un produit cartésien entre un groupe quotient et un sous groupe d'un groupe donné, me disait sans cesse que j'allais faire des produits erronés entre des classes d'équivalence éléments de G/H et des éléments de H, alors qu'en réalité, la loi induite sur G/H*H faisait des produits entre des classes d'équivalences d'un côté et des éléments de H de l'autre.
Je m'excuse pour ce désagrément, et je vous remercie amplement: ce genre de raisonnement irraisonnable m'a créé beaucoup d'ennuis avec mes professeurs depuis le collège, mais je vous demande à vous et aux autres professeurs du site d'être indulgents et magnanime.
Une dernière chose, le "f" que vous avez remarqué est un petit poisson qui a passé entre les mailles d'un copier-coller, quand j'ai rédigé mon intervention: je le corrigerai tout de suite.
Encore une fois, Merci.
Re: theorie des groupe
Bonjour;
pour terminer ce que j'ai commencé hier, et après avoir longuement tenté de trouver le contre-exemple avec le Groupe de Klein, je me suis orienté vers le groupe cyclique d'ordre 4, et "Eurêka" je crois que je l'ai trouvé:
Notons G le groupe cyclique d'ordre 4 tel que avec e l'élément neutre du groupe. Parmi les sous-groupes de G d'ordre 2, on trouve le sous-groupe distingué
avec e l'élément neutre du groupe. Parmi les sous-groupes de G d'ordre 2, on trouve le sous-groupe distingué  .
.
La table de Cayley de H est:
 .
.
On trouve aussi

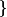 avec
avec  et
et  .
.
La table de Cayley de G/H est:
 ,
,
donc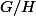 x
x 
, (\dot e,u^2), (\dot u,e), (\dot u,u^2)\}) ,
,
est un groupe d'ordre 4 dont la table de Cayley montre que c'est un groupe de Klein.
Le groupe de Klein n'est pas cyclique alors que G l'est, donc n'est pas isomorphe à
n'est pas isomorphe à 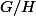 x
x  , d’où le contre-exemple cherché.
, d’où le contre-exemple cherché.
Si j'y suis arrivé, c'est grâce à vous M.Robot, donc Merci, Merci et Merci.
pour terminer ce que j'ai commencé hier, et après avoir longuement tenté de trouver le contre-exemple avec le Groupe de Klein, je me suis orienté vers le groupe cyclique d'ordre 4, et "Eurêka" je crois que je l'ai trouvé:
Notons G le groupe cyclique d'ordre 4 tel que
La table de Cayley de H est:
On trouve aussi
La table de Cayley de G/H est:
donc
est un groupe d'ordre 4 dont la table de Cayley montre que c'est un groupe de Klein.
Le groupe de Klein n'est pas cyclique alors que G l'est, donc
Si j'y suis arrivé, c'est grâce à vous M.Robot, donc Merci, Merci et Merci.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
