Développement limité en un point a
14 messages
- Page 1 sur 1
Développement limité en un point a
Bonjour,
Je ne comprends pas comment faire un développement limité en un point a, à partir des DL usuels en 0.
J'ai beau chercher, je ne trouve pas de cours à ce propos que je comprends.
Un peu d'aide ?
Merci beaucoup !
Je ne comprends pas comment faire un développement limité en un point a, à partir des DL usuels en 0.
J'ai beau chercher, je ne trouve pas de cours à ce propos que je comprends.
Un peu d'aide ?
Merci beaucoup !
Re: Développement limité en un point a
Salut !
Le mieux serait que tu nous donnes un exemple concret d'endroit où tu bloques.
Les DL en un point a sont obtenus comme translation des DL en point 0.
Par exemple, un DL en 0 d'ordre 2 de l'exponentielle est :) donc un DL en a d'ordre 2 de l'exponentielle est :
donc un DL en a d'ordre 2 de l'exponentielle est : +(x-a)^2+o((x-a)^2)) .
.

Le mieux serait que tu nous donnes un exemple concret d'endroit où tu bloques.
Les DL en un point a sont obtenus comme translation des DL en point 0.
Par exemple, un DL en 0 d'ordre 2 de l'exponentielle est :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Développement limité en un point a
Salut,
Un exemple :}{x^2}) en 1 à l'ordre 3.
en 1 à l'ordre 3.
Par ailleurs :
Quand on demande de trouver une limite en d'une fonction f, je suppose qu'il faille faire le DL en
d'une fonction f, je suppose qu'il faille faire le DL en  , puis en faire la limite quand x tend vers
, puis en faire la limite quand x tend vers  . Mais, je ne sais pas faire de DL en
. Mais, je ne sais pas faire de DL en  .
.
Un exemple :
Par ailleurs :
Quand on demande de trouver une limite en
Re: Développement limité en un point a
Les DL ne sont se font uniquement au voisinage d'un point fini : pas au voisinage de l'infini.
Pour ton exemple, tu fais un DL en 0 à l'ordre 3, puis tu "translates" d'une unité pour avoir ton DL en 1 à l'ordre 3.
Quel est le DL en 0 à l'ordre 3 de ton quotient ? Si j'appelle f(x) ce DL en 0 à l'ordre 3, le DL en 1 à l'ordre 3 sera f(x-1).
Pour ton exemple, tu fais un DL en 0 à l'ordre 3, puis tu "translates" d'une unité pour avoir ton DL en 1 à l'ordre 3.
Quel est le DL en 0 à l'ordre 3 de ton quotient ? Si j'appelle f(x) ce DL en 0 à l'ordre 3, le DL en 1 à l'ordre 3 sera f(x-1).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Développement limité en un point a
Salut,
Personnellement, je trouve que pour faire un DL de en
en 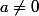 , le mieux est de poser une nouvelle variable
, le mieux est de poser une nouvelle variable 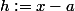 et de faire un développement limité en
et de faire un développement limité en  pour la variable
pour la variable  cette fois-ci.
cette fois-ci.
Dans ton exemple, tu peux te ramener au DL de}{(h+1)^2}) au voisinage de
au voisinage de  (en remarquant notamment que
(en remarquant notamment que  = \ln (2) + \ln (1+\frac{h}{2})) ).
).
En remplaçant ensuite par
par  tu obtiens ton DL en
tu obtiens ton DL en 

Personnellement, je trouve que pour faire un DL de
Dans ton exemple, tu peux te ramener au DL de
En remplaçant ensuite
Re: Développement limité en un point a
Ok merci à vous deux !
Je pense avoir compris le principe, je m'entrainerai demain avec quelques exemples.
Et pour déterminer une limite en avec les DL on fait comment ?
avec les DL on fait comment ?
Je pense avoir compris le principe, je m'entrainerai demain avec quelques exemples.
Et pour déterminer une limite en
Re: Développement limité en un point a
Par définition les DL se font au voisinage d'un point fini et sont des développements locaux. Par conséquent il n'est pas possible d'obtenir une limite en 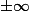 à l'aide de DL. Pour cela on utilise des équivalents.
à l'aide de DL. Pour cela on utilise des équivalents.
Edit : En posant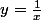 on peut se ramener au voisinage de
on peut se ramener au voisinage de  . Néanmoins aux infinis on parle plus de DA (asymptotique) que de DL. Il faut aussi veiller au signe de
. Néanmoins aux infinis on parle plus de DA (asymptotique) que de DL. Il faut aussi veiller au signe de  .
.
Edit : En posant
Modifié en dernier par samoufar le 29 Mai 2016, 08:57, modifié 1 fois.
Re: Développement limité en un point a
Pour 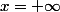 tu fais un développement limité pour la variable
tu fais un développement limité pour la variable 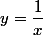 au voisinage de
au voisinage de 
Re: Développement limité en un point a
salut
f(x) = ln(1 + x)/x²
posons x = 1 + y donc x --> 1 <=> y --> 0
g(y) = f(x) = ln(2 + y)(1 + y)²
faire un dl de f en 1 à l'ordre n <=> faire un dl de g en 0 à l'ordre n
puis remplacer y par x - 1 dans le dl de g en 0
f(x) = ln(1 + x)/x²
posons x = 1 + y donc x --> 1 <=> y --> 0
g(y) = f(x) = ln(2 + y)(1 + y)²
faire un dl de f en 1 à l'ordre n <=> faire un dl de g en 0 à l'ordre n
puis remplacer y par x - 1 dans le dl de g en 0
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Développement limité en un point a
Merci pour vos réponses. 
Et pour une question de ce type, quelles sont les étapes ?
Rechercher les asymptotes au graphe de la fonction g définie sur R⋆ par = \frac{x}{1+e^{\frac{1}{x}}})
Et pour une question de ce type, quelles sont les étapes ?
Rechercher les asymptotes au graphe de la fonction g définie sur R⋆ par
Re: Développement limité en un point a
lim exp(1/x) = 1 quand x --> +-oo donc en +-oo donc asymptote d'équation y = x/2 + b
posons h = 1/x alors x --> +-oo <=> h --> 0
exp(h) = 1 + h + h²/2 + o(h²)
1/(1 + exp h) = (1/2) * 1/[1 + h/2 + h²/4 + o(h²)] = (1/2)[1 - h/2 - h²/4 + o(h)] = (1/2)[1 - 1/2x - 1/4x² + o(1/x²)]
et en multipliant par x : g(x) = (1/2)[x - 1/2 - 1/4x + o(1/x)]
....
posons h = 1/x alors x --> +-oo <=> h --> 0
exp(h) = 1 + h + h²/2 + o(h²)
1/(1 + exp h) = (1/2) * 1/[1 + h/2 + h²/4 + o(h²)] = (1/2)[1 - h/2 - h²/4 + o(h)] = (1/2)[1 - 1/2x - 1/4x² + o(1/x²)]
et en multipliant par x : g(x) = (1/2)[x - 1/2 - 1/4x + o(1/x)]
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Développement limité en un point a
capitaine nuggets a écrit:Salut !
Le mieux serait que tu nous donnes un exemple concret d'endroit où tu bloques.
Les DL en un point a sont obtenus comme translation des DL en point 0.
Par exemple, un DL en 0 d'ordre 2 de l'exponentielle est :donc un DL en a d'ordre 2 de l'exponentielle est :
.
@capitaine nuggets
Il me semble que le DL en a à l'ordre 2 de l'exponentielle de x est :
Re: Développement limité en un point a
oui l'exponentielle possède ces deux propriétés intéressantes que :
elle est sa dérivée
l'exponentielle d'une somme est le produit des exponentielles
donc :
quand x tend vers a alors h = x - a tend vers 0 donc un dl de exp (x) quand x tend vers a s'obtient par produit du dl de exp (h) en 0 par exp (a) puisque

et il manque un facteur 1/2 dans vos dl ....
elle est sa dérivée
l'exponentielle d'une somme est le produit des exponentielles
donc :
quand x tend vers a alors h = x - a tend vers 0 donc un dl de exp (x) quand x tend vers a s'obtient par produit du dl de exp (h) en 0 par exp (a) puisque
et il manque un facteur 1/2 dans vos dl ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

